Printing all solutions in N-Queen Problem

Difficulty Level : Hard
Last Updated : 23 Jul, 2021

The N Queen is the problem of placing N chess queens on an N×N chessboard so that no two queens attack each other. For example, following is a solution for 4 Queen problem.
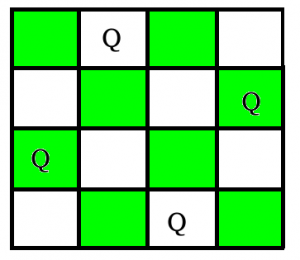
The N Queen is the problem of placing N chess queens on an N×N chessboard so that no two queens attack each other. For example, following are two solutions for 4 Queen problem.

nQueen-solution2

In previous post, we have discussed an approach that prints only one possible solution, so now in this post, the task is to print all solutions in N-Queen Problem. Each solution contains distinct board configurations of the N-queens’ placement, where the solutions are a permutation of [1,2,3..n] in increasing order, here the number in the ith place denotes that the ith-column queen is placed in the row with that number. For the example above solution is written as [[2 4 1 3 ] [3 1 4 2 ]]. The solution discussed here is an extension of the same approach.

Backtracking Algorithm

The idea is to place queens one by one in different columns, starting from the leftmost column. When we place a queen in a column, we check for clashes with already placed queens. In the current column, if we find a row for which there is no clash, we mark this row and column as part of the solution. If we do not find such a row due to clashes then we backtrack and return false.

1) Start in the leftmost column
2) If all queens are placed
    return true
3) Try all rows in the current column.  Do following
   for every tried row.
    a) If the queen can be placed safely in this row
       then mark this [row, column] as part of the 
       solution and recursively check if placing  
       queen here leads to a solution.
    b) If placing queen in [row, column] leads to a
       solution then return true.
    c) If placing queen doesn't lead to a solution 
       then unmark this [row, column] (Backtrack) 
       and go to step (a) to try other rows.
3) If all rows have been tried and nothing worked, 
   return false to trigger backtracking.

A modification is that we can find whether we have a previously placed queen in a column or in left diagonal or in right diagonal in O(1) time. We can observe that
1)For all cells in a particular left diagonal , their row + col = constant.
2)For all cells in a particular right diagonal, their row – col + n – 1 = constant.

Let say n = 5, then we have a total of 2n-1 left and right diagonals

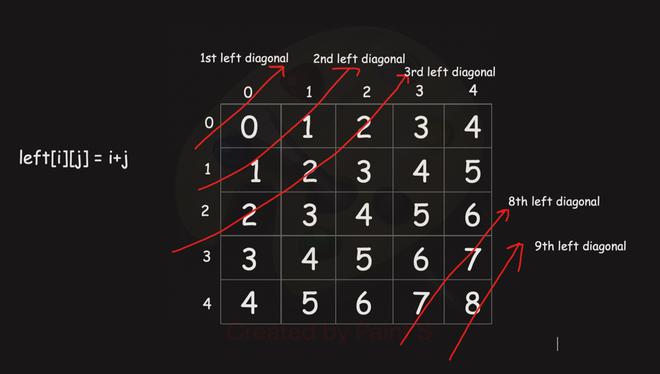
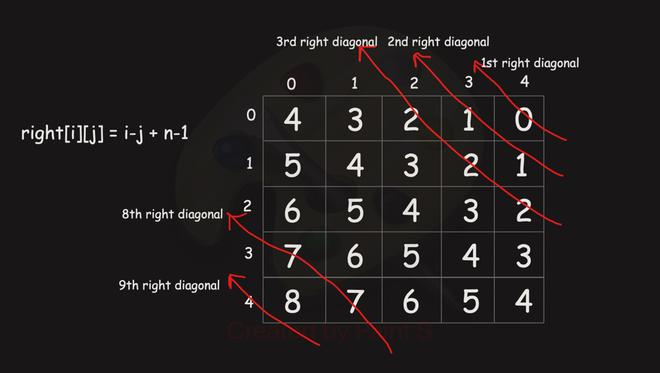
Let say we placed a queen at (2,0)

(2,0) have leftDiagonal value = 2. Now we can not place another queen at (1,1) and (0,2) because both of these have same leftDiagonal value as for (2,0). Similar thing can be noticed for right diagonal as well.

C++

/* C/C++ program to solve N Queen Problem using
backtracking */
#include <bits/stdc++.h>
using namespace std;
 
vector<vector<int> > result;
 
/* A utility function to check if a queen can
be placed on board[row][col]. Note that this
function is called when "col" queens are
already placed in columns from 0 to col -1.
So we need to check only left side for
attacking queens */
bool isSafe(vector<vector<int> > board,
            int row, int col)
{
    int i, j;
    int N = board.size();
 
    /* Check this row on left side */
    for (i = 0; i < col; i++)
        if (board[row][i])
            return false;
 
    /* Check upper diagonal on left side */
    for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
        if (board[i][j])
            return false;
 
    /* Check lower diagonal on left side */
    for (i = row, j = col; j >= 0 && i < N; i++, j--)
        if (board[i][j])
            return false;
 
    return true;
}
 
/* A recursive utility function to solve N
Queen problem */
bool solveNQUtil(vector<vector<int> >& board, int col)
{
    /* base case: If all queens are placed
    then return true */
    int N = board.size();
    if (col == N) {
        vector<int> v;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                if (board[i][j] == 1)
                    v.push_back(j + 1);
            }
        }
        result.push_back(v);
        return true;
    }
 
    /* Consider this column and try placing
    this queen in all rows one by one */
    bool res = false;
    for (int i = 0; i < N; i++) {
        /* Check if queen can be placed on
        board[i][col] */
        if (isSafe(board, i, col)) {
            /* Place this queen in board[i][col] */
            board[i][col] = 1;
 
            // Make result true if any placement
            // is possible
            res = solveNQUtil(board, col + 1) || res;
 
            /* If placing queen in board[i][col]
            doesn't lead to a solution, then
            remove queen from board[i][col] */
            board[i][col] = 0; // BACKTRACK
        }
    }
 
    /* If queen can not be place in any row in
        this column col then return false */
    return res;
}
 
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
 
vector<vector<int> > nQueen(int n)
{
    result.clear();
    vector<vector<int> > board(n, vector<int>(n, 0));
 
    if (solveNQUtil(board, 0) == false) {
        return {};
    }
 
    sort(result.begin(), result.end());
    return result;
}
 
// Driver Code
int main()
{
    int n = 4;
    vector<vector<int> > v = nQueen(n);
 
    for (auto ar : v) {
        cout << "[";
        for (auto it : ar)
            cout << it << " ";
        cout << "]";
    }
 
    return 0;
}

Java

/* Java program to solve N Queen
Problem using backtracking */
import java.util.*;
class GfG {
  
  /* This function solves the N Queen problem using
    Backtracking. It mainly uses solveNQUtil() to
    solve the problem.
    */
    static List<List<Integer>> nQueen(int n) {
       // cols[i] = true if there is a queen previously placed at ith column
        cols = new boolean[n];
        // leftDiagonal[i] = true if there is a queen previously placed at
          // i = (row + col )th left diagonal
        leftDiagonal = new boolean[2*n];
          // rightDiagonal[i] = true if there is a queen previously placed at
          // i = (row - col + n - 1)th rightDiagonal diagonal
        rightDiagonal = new boolean[2*n];
        result  = new ArrayList<>();
        List<Integer> temp = new ArrayList<>();
        for(int i=0;i<n;i++)temp.add(0);
        solveNQUtil(result,n,0,temp);
         
        return result;
    }
    private static void solveNQUtil(List<List<Integer>> result,int n,int row,List<Integer> comb){
        if(row==n){
          // if row==n it means we have successfully placed all n queens.
          // hence add current arrangement to our answer
          // comb represent current combination
            result.add(new ArrayList<>(comb));
            return;
        }
        for(int col = 0;col<n;col++){
           // if we have a queen previously placed in the current column
           // or in current left or right diagonal we continue
            if(cols[col] || leftDiagonal[row+col] || rightDiagonal[row-col+n])
                continue;
           // otherwise we place a queen at cell[row][col] and
           //make current column, left diagonal and righ diagonal true
            cols[col] = leftDiagonal[row+col] = rightDiagonal[row-col+n] = true;
            comb.set(col,row+1);
            // then we goto next row
            solveNQUtil(result,n,row+1,comb);
            // then we backtrack and remove our currently placed queen
            cols[col] = leftDiagonal[row+col] = rightDiagonal[row-col+n] = false;
        }
    }
  static List<List<Integer> > result
        = new ArrayList<List<Integer> >();
   static boolean[] cols,leftDiagonal,rightDiagonal;
 
    // Driver code
    public static void main(String[] args)
    {
        int n = 4;
 
        List<List<Integer> > res = nQueen(n);
        System.out.println(res);
    }
}

Python3

''' Python3 program to solve N Queen Problem using
backtracking '''
 
 
result = []
 
# A utility function to print solution
 
 
''' A utility function to check if a queen can
be placed on board[row][col]. Note that this
function is called when "col" queens are
already placed in columns from 0 to col -1.
So we need to check only left side for
attacking queens '''
 
 
def isSafe(board, row, col):
 
    # Check this row on left side
    for i in range(col):
        if (board[row][i]):
            return False
 
    # Check upper diagonal on left side
    i = row
    j = col
    while i >= 0 and j >= 0:
        if(board[i][j]):
            return False
        i -= 1
        j -= 1
 
    # Check lower diagonal on left side
    i = row
    j = col
    while j >= 0 and i < 4:
        if(board[i][j]):
            return False
        i = i + 1
        j = j - 1
 
    return True
 
 
''' A recursive utility function to solve N
Queen problem '''
 
 
def solveNQUtil(board, col):
    ''' base case: If all queens are placed
    then return true '''
    if (col == 4):
        v = []
        for i in board:
          for j in range(len(i)):
            if i[j] == 1:
              v.append(j+1)
        result.append(v)
        return True
 
    ''' Consider this column and try placing
    this queen in all rows one by one '''
    res = False
    for i in range(4):
 
        ''' Check if queen can be placed on
        board[i][col] '''
        if (isSafe(board, i, col)):
 
            # Place this queen in board[i][col]
            board[i][col] = 1
 
            # Make result true if any placement
            # is possible
            res = solveNQUtil(board, col + 1) or res
 
            ''' If placing queen in board[i][col]
            doesn't lead to a solution, then
            remove queen from board[i][col] '''
            board[i][col] = 0  # BACKTRACK
 
    ''' If queen can not be place in any row in
        this column col then return false '''
    return res
 
 
''' This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.'''
 
 
def solveNQ(n):
    result.clear()
    board = [[0 for j in range(n)]
             for i in range(n)]
    solveNQUtil(board, 0)
    result.sort()
    return result
 
 
# Driver Code
n = 4
res = solveNQ(n)
print(res)
 
# This code is contributed by YatinGupta

C#

/* C# program to solve N Queen
Problem using backtracking */
using System;
using System.Collections;
using System.Collections.Generic;
 
class GfG {
 
    static List<List<int> > result = new List<List<int> >();
 
    /* A utility function to check if a queen can
    be placed on board[row,col]. Note that this
    function is called when "col" queens are
    already placed in columns from 0 to col -1.
    So we need to check only left side for
    attacking queens */
    static bool isSafe(int[, ] board, int row, int col,
                       int N)
    {
        int i, j;
 
        /* Check this row on left side */
        for (i = 0; i < col; i++)
            if (board[row, i] == 1)
                return false;
 
        /* Check upper diagonal on left side */
        for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
            if (board[i, j] == 1)
                return false;
 
        /* Check lower diagonal on left side */
        for (i = row, j = col; j >= 0 && i < N; i++, j--)
            if (board[i, j] == 1)
                return false;
 
        return true;
    }
 
    /* A recursive utility function
    to solve N Queen problem */
    static bool solveNQUtil(int[, ] board, int col, int N)
    {
        /* base case: If all queens are placed
        then return true */
 
        if (col == N) {
            List<int> v = new List<int>();
            for (int i = 0; i < N; i++)
                for (int j = 0; j < N; j++) {
                    if (board[i, j] == 1)
                        v.Add(j + 1);
                }
            result.Add(v);
            return true;
        }
 
        /* Consider this column and try placing
        this queen in all rows one by one */
        bool res = false;
        for (int i = 0; i < N; i++) {
            /* Check if queen can be placed on
            board[i,col] */
            if (isSafe(board, i, col, N)) {
                /* Place this queen in board[i,col] */
                board[i, col] = 1;
 
                // Make result true if any placement
                // is possible
                res = solveNQUtil(board, col + 1, N) || res;
 
                /* If placing queen in board[i,col]
                doesn't lead to a solution, then
                remove queen from board[i,col] */
                board[i, col] = 0; // BACKTRACK
            }
        }
 
        /* If queen can not be place in any row in
            this column col then return false */
        return res;
    }
 
    /* This function solves the N Queen problem using
    Backtracking. It mainly uses solveNQUtil() to
    solve the problem. It returns false if queens
    cannot be placed, otherwise return true and
    prints placement of queens in the form of 1s.
    Please note that there may be more than one
    solutions, this function prints one of the
    feasible solutions.*/
    static List<List<int> > solveNQ(int n)
    {
        result.Clear();
        int[, ] board = new int[n, n];
 
        solveNQUtil(board, 0, n);
        return result;
    }
 
    // Driver code
    public static void Main()
    {
        int n = 4;
        List<List<int> > res = solveNQ(n);
        for (int i = 0; i < res.Count; i++) {
            Console.Write("[");
            for (int j = 0; j < res[i].Count; j++) {
                Console.Write(res[i][j]+ " ");
            }
            Console.Write("]");
        }
    }
}
 
/* This code contributed by PrinciRaj1992 */

Output

[2 4 1 3 ][3 1 4 2 ]

Efficient Backtracking Approach Using Bit-Masking

Algorithm:
There is always only one queen in each row and each column, so idea of backtracking is to start placing queen from the leftmost column of each row and find a column where the queen could be placed without collision with previously placed queens. It is repeated from the first row till the last row. While placing a queen, it is tracked as if it is not making a collision (row-wise, column-wise and diagonally) with queens placed in previous rows. Once it is found that the queen can’t be placed at a particular column index in a row, the algorithm backtracks and change the position of the queen placed in the previous row then moves forward to place the queen in the next row.

Start with three-bit vector which is used to track safe place for queen placement row-wise, column-wise and diagonally in each iteration.
Three-bit vector will contain information as bellow:
- rowmask: set bit index (i) of this bit vector will indicate, the queen can’t be placed at ith column of next row.
- ldmask: set bit index (i) of this bit vector will indicate, the queen can’t e placed at ith column of next row. It represents the unsafe column index for next row falls under left diagonal of queens placed in previous rows.
- rdmask: set bit index (i) of this bit vector will indicate, the queen can’t be placed at ith column of next row. It represents the unsafe column index for next row falls right diagonal of queens placed in previous rows.
There is a 2-D (NxN) matrix (board), which will have ‘ ‘ character at all indexes in beginning and it gets filled by ‘Q’ row-by-row. Once all rows are filled by ‘Q’, the current solution is pushed into the result list.

Below is the implementation of the above approach:

C++

// CPP program for above approach
#include <bits/stdc++.h>
 
using namespace std;
 
vector<vector<int> > result;
// Program to solve N Quuens problem
void solveBoard(vector<vector<char> >& board, int row,
                int rowmask, int ldmask, int rdmask,
                int& ways)
{
 
    int n = board.size();
 
    // All_rows_filled is a bit mask having all N bits set
    int all_rows_filled = (1 << n) - 1;
 
    // If rowmask will have all bits set, means queen has
    // been placed successfully in all rows and board is
    // displayed
    if (rowmask == all_rows_filled) {
 
        vector<int> v;
        for (int i = 0; i < board.size(); i++) {
            for (int j = 0; j < board.size(); j++) {
                if (board[i][j] == 'Q')
                    v.push_back(j + 1);
            }
        }
        result.push_back(v);
        return;
    }
 
    // We extract a bit mask(safe) by rowmask,
    // ldmask and rdmask. all set bits of 'safe'
    // indicates the safe column index for queen
    // placement of this iteration for row index(row).
    int safe
        = all_rows_filled & (~(rowmask | ldmask | rdmask));
    while (safe) {
 
        // Extracts the right-most set bit
        // (safe column index) where queen
        // can be placed for this row
        int p = safe & (-safe);
        int col = (int)log2(p);
        board[row][col] = 'Q';
 
        // This is very important:
        // we need to update rowmask, ldmask and rdmask
        // for next row as safe index for queen placement
        // will be decided by these three bit masks.
 
        // We have all three rowmask, ldmask and
        // rdmask as 0 in beginning. Suppose, we are placing
        // queen at 1st column index at 0th row. rowmask,
        // ldmask and rdmask will change for next row as
        // below:
 
        // rowmask's 1st bit will be set by OR operation
        // rowmask = 00000000000000000000000000000010
 
        // ldmask will change by setting 1st
        // bit by OR operation  and left shifting
        // by 1 as it has to block the next column
        // of next row because that will fall on left
        // diagonal. ldmask =
        // 00000000000000000000000000000100
 
        // rdmask will change by setting 1st bit
        // by OR operation and right shifting by 1
        // as it has to block the previous column
        // of next row because that will fall on right
        // diagonal. rdmask =
        // 00000000000000000000000000000001
 
        // these bit masks will keep updated in each
        // iteration for next row
        solveBoard(board, row + 1, rowmask | p,
                   (ldmask | p) << 1, (rdmask | p) >> 1,
                   ways);
 
        // Reset right-most set bit to 0 so,
        // next iteration will continue by placing the queen
        // at another safe column index of this row
        safe = safe & (safe - 1);
 
        // Backtracking, replace 'Q' by ' '
        board[row][col] = ' ';
    }
    return;
}
 
// Driver Code
int main()
{
    // Board size
    int n = 4;
    int ways = 0;
 
    vector<vector<char> > board;
    for (int i = 0; i < n; i++) {
        vector<char> tmp;
        for (int j = 0; j < n; j++) {
            tmp.push_back(' ');
        }
        board.push_back(tmp);
    }
 
    int rowmask = 0, ldmask = 0, rdmask = 0;
    int row = 0;
 
    // Function Call
    result.clear();
    solveBoard(board, row, rowmask, ldmask, rdmask, ways);
    sort(result.begin(),result.end());
    for (auto ar : result) {
        cout << "[";
        for (auto it : ar)
            cout << it << " ";
        cout << "]";
    }
    return 0;
}
// This code is contributed by Nikhil Vinay

Java

// Java Program for aove approach
import java.util.*;
public class NQueenSolution {
 
    static List<List<Integer> > result
        = new ArrayList<List<Integer> >();
 
    // Program to solve N-Queens Problem
    public void solveBoard(char[][] board, int row,
                           int rowmask, int ldmask,
                           int rdmask)
    {
        int n = board.length;
 
        // All_rows_filled is a bit mask
        // having all N bits set
        int all_rows_filled = (1 << n) - 1;
 
        // If rowmask will have all bits set,
        // means queen has been placed successfully
        // in all rows and board is displayed
        if (rowmask == all_rows_filled) {
            List<Integer> v = new ArrayList<>();
 
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if (board[i][j] == 'Q')
                        v.add(j + 1);
                }
            }
            result.add(v);
            return;
        }
 
        // We extract a bit mask(safe) by rowmask,
        // ldmask and rdmask. all set bits of 'safe'
        // indicates the safe column index for queen
        // placement of this iteration for row index(row).
        int safe = all_rows_filled
                   & (~(rowmask | ldmask | rdmask));
        while (safe > 0) {
 
            // Extracts the right-most set bit
            // (safe column index) where queen
            // can be placed for this row
            int p = safe & (-safe);
            int col = (int)(Math.log(p) / Math.log(2));
            board[row][col] = 'Q';
 
            // This is very important:
            // we need to update rowmask, ldmask and rdmask
            // for next row as safe index for queen
            // placement will be decided by these three bit
            // masks.
 
            // We have all three rowmask, ldmask and
            // rdmask as 0 in beginning. Suppose, we are
            // placing queen at 1st column index at 0th row.
            // rowmask, ldmask and rdmask will change for
            // next row as below:
 
            // rowmask's 1st bit will be set by OR operation
            // rowmask = 00000000000000000000000000000010
 
            // ldmask will change by setting 1st
            // bit by OR operation  and left shifting
            // by 1 as it has to block the next column
            // of next row because that will fall on left
            // diagonal. ldmask =
            // 00000000000000000000000000000100
 
            // rdmask will change by setting 1st bit
            // by OR operation and right shifting by 1
            // as it has to block the previous column
            // of next row because that will fall on right
            // diagonal. rdmask =
            // 00000000000000000000000000000001
 
            // these bit masks will keep updated in each
            // iteration for next row
            solveBoard(board, row + 1, rowmask | p,
                       (ldmask | p) << 1,
                       (rdmask | p) >> 1);
 
            // Reset right-most set bit to 0 so,
            // next iteration will continue by placing the
            // queen at another safe column index of this
            // row
            safe = safe & (safe - 1);
 
            // Backtracking, replace 'Q' by ' '
            board[row][col] = ' ';
        }
    }
 
    // Program to print board
    public void printBoard(char[][] board)
    {
        for (int i = 0; i < board.length; i++) {
            System.out.print("|");
            for (int j = 0; j < board[i].length; j++) {
                System.out.print(board[i][j] + "|");
            }
            System.out.println();
        }
    }
 
    // Driver Code
    public static void main(String args[])
    {
 
        // Board size
        int n = 4;
 
        char board[][] = new char[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                board[i][j] = ' ';
            }
        }
 
        int rowmask = 0, ldmask = 0, rdmask = 0;
        int row = 0;
 
        NQueenSolution solution = new NQueenSolution();
 
        // Function Call
        result.clear();
        solution.solveBoard(board, row, rowmask, ldmask,
                            rdmask);
        System.out.println(result);
    }
}
 
// This code is contributed by Nikhil Vinay

Python3

# Python program for above approach
import math
 
result = []
 
# Program to solve N-Queens Problem
 
 
def solveBoard(board, row, rowmask,
               ldmask, rdmask):
 
    n = len(board)
 
    # All_rows_filled is a bit mask
    # having all N bits set
    all_rows_filled = (1 << n) - 1
 
    # If rowmask will have all bits set, means
    # queen has been placed successfully
    # in all rows and board is displayed
    if (rowmask == all_rows_filled):
        v = []
        for i in board:
            for j in range(len(i)):
                if i[j] == 'Q':
                    v.append(j+1)
        result.append(v)
 
    # We extract a bit mask(safe) by rowmask,
    # ldmask and rdmask. all set bits of 'safe'
    # indicates the safe column index for queen
    # placement of this iteration for row index(row).
    safe = all_rows_filled & (~(rowmask |
                                ldmask | rdmask))
 
    while (safe > 0):
 
        # Extracts the right-most set bit
        # (safe column index) where queen
        # can be placed for this row
        p = safe & (-safe)
        col = (int)(math.log(p)/math.log(2))
        board[row][col] = 'Q'
 
        # This is very important:
        # we need to update rowmask, ldmask and rdmask
        # for next row as safe index for queen placement
        # will be decided by these three bit masks.
 
        # We have all three rowmask, ldmask and
        # rdmask as 0 in beginning. Suppose, we are placing
        # queen at 1st column index at 0th row. rowmask, ldmask
        # and rdmask will change for next row as below:
 
        # rowmask's 1st bit will be set by OR operation
        # rowmask = 00000000000000000000000000000010
 
        # ldmask will change by setting 1st
        # bit by OR operation  and left shifting
        # by 1 as it has to block the next column
        # of next row because that will fall on left diagonal.
        # ldmask = 00000000000000000000000000000100
 
        # rdmask will change by setting 1st bit
        # by OR operation and right shifting by 1
        # as it has to block the previous column
        # of next row because that will fall on right diagonal.
        # rdmask = 00000000000000000000000000000001
 
        # these bit masks will keep updated in each
        # iteration for next row
        solveBoard(board, row+1, rowmask | p,
                   (ldmask | p) << 1, (rdmask | p) >> 1)
 
        # Reset right-most set bit to 0 so, next
        # iteration will continue by placing the queen
        # at another safe column index of this row
        safe = safe & (safe-1)
 
        # Backtracking, replace 'Q' by ' '
        board[row][col] = ' '
 
# Program to print board
 
 
def printBoard(board):
    for row in board:
        print("|" + "|".join(row) + "|")
 
# Driver Code
 
 
def main():
 
    n = 4  # board size
    board = []
 
    for i in range(n):
        row = []
        for j in range(n):
            row.append(' ')
        board.append(row)
 
    rowmask = 0
    ldmask = 0
    rdmask = 0
    row = 0
 
    # Function Call
    result.clear()
    solveBoard(board, row, rowmask, ldmask, rdmask)
    result.sort()
    print(result)
 
 
if __name__ == "__main__":
    main()
 
# This code is contributed by Nikhil Vinay

Output

[2 4 1 3 ][3 1 4 2 ]

This article is contributed by Sahil Chhabra. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.

My Personal Notes