Printing Items in 0/1 Knapsack
Last Updated :
23 Jun, 2022
Given weights and values of n items, put these items in a knapsack of capacity W to get the maximum total value in the knapsack. In other words, given two integer arrays, val[0..n-1] and wt[0..n-1] represent values and weights associated with n items respectively. Also given an integer W which represents knapsack capacity, find out the items such that sum of the weights of those items of a given subset is smaller than or equal to W. You cannot break an item, either pick the complete item or don’t pick it (0-1 property).
Prerequisite : 0/1 Knapsack
Examples :
Input : val[] = {60, 100, 120};
wt[] = {10, 20, 30};
W = 50;
Output : 220 //maximum value that can be obtained
30 20 //weights 20 and 30 are included.
Input : val[] = {40, 100, 50, 60};
wt[] = {20, 10, 40, 30};
W = 60;
Output : 200
30 20 10
Approach :
Let val[] = {1, 4, 5, 7}, wt[] = {1, 3, 4, 5}
W = 7.
The 2d knapsack table will look like :
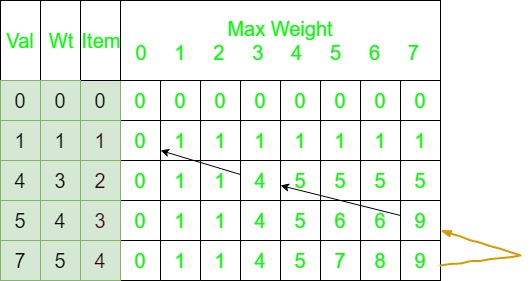
Start backtracking from K[n][W].Here K[n][W] is 9.
Since this value comes from the top (shown by grey arrow), the item in this row is not included. Go vertically upward in the table without including this in the knapsack. Now, this value K[n-1][W] which is 9 doesn’t come from the top which means the item in this row is included and go vertically up and then left by the weight of the included item ( shown by black arrow). Continuing this process include weights 3 and 4 with a total value 9 in the knapsack.
C++
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
int max(int a, int b) { return (a > b) ? a : b; }
void printknapSack(int W, int wt[], int val[], int n)
{
int i, w;
int K[n + 1][W + 1];
for (i = 0; i <= n; i++) {
for (w = 0; w <= W; w++) {
if (i == 0 || w == 0)
K[i][w] = 0;
else if (wt[i - 1] <= w)
K[i][w] = max(val[i - 1] +
K[i - 1][w - wt[i - 1]], K[i - 1][w]);
else
K[i][w] = K[i - 1][w];
}
}
int res = K[n][W];
cout<< res << endl;
w = W;
for (i = n; i > 0 && res > 0; i--) {
if (res == K[i - 1][w])
continue;
else {
cout<<" "<<wt[i - 1] ;
res = res - val[i - 1];
w = w - wt[i - 1];
}
}
}
int main()
{
int val[] = { 60, 100, 120 };
int wt[] = { 10, 20, 30 };
int W = 50;
int n = sizeof(val) / sizeof(val[0]);
printknapSack(W, wt, val, n);
return 0;
}
|
C
#include <stdio.h>
int max(int a, int b) { return (a > b) ? a : b; }
void printknapSack(int W, int wt[], int val[], int n)
{
int i, w;
int K[n + 1][W + 1];
for (i = 0; i <= n; i++) {
for (w = 0; w <= W; w++) {
if (i == 0 || w == 0)
K[i][w] = 0;
else if (wt[i - 1] <= w)
K[i][w] = max(val[i - 1] +
K[i - 1][w - wt[i - 1]], K[i - 1][w]);
else
K[i][w] = K[i - 1][w];
}
}
int res = K[n][W];
printf("%d\n", res);
w = W;
for (i = n; i > 0 && res > 0; i--) {
if (res == K[i - 1][w])
continue;
else {
printf("%d ", wt[i - 1]);
res = res - val[i - 1];
w = w - wt[i - 1];
}
}
}
int main()
{
int val[] = { 60, 100, 120 };
int wt[] = { 10, 20, 30 };
int W = 50;
int n = sizeof(val) / sizeof(val[0]);
printknapSack(W, wt, val, n);
return 0;
}
|
Java
class GFG {
static int max(int a, int b)
{
return (a > b) ? a : b;
}
static void printknapSack(int W, int wt[],
int val[], int n)
{
int i, w;
int K[][] = new int[n + 1][W + 1];
for (i = 0; i <= n; i++) {
for (w = 0; w <= W; w++) {
if (i == 0 || w == 0)
K[i][w] = 0;
else if (wt[i - 1] <= w)
K[i][w] = Math.max(val[i - 1] +
K[i - 1][w - wt[i - 1]], K[i - 1][w]);
else
K[i][w] = K[i - 1][w];
}
}
int res = K[n][W];
System.out.println(res);
w = W;
for (i = n; i > 0 && res > 0; i--) {
if (res == K[i - 1][w])
continue;
else {
System.out.print(wt[i - 1] + " ");
res = res - val[i - 1];
w = w - wt[i - 1];
}
}
}
public static void main(String arg[])
{
int val[] = { 60, 100, 120 };
int wt[] = { 10, 20, 30 };
int W = 50;
int n = val.length;
printknapSack(W, wt, val, n);
}
}
|
Python3
def printknapSack(W, wt, val, n):
K = [[0 for w in range(W + 1)]
for i in range(n + 1)]
for i in range(n + 1):
for w in range(W + 1):
if i == 0 or w == 0:
K[i][w] = 0
elif wt[i - 1] <= w:
K[i][w] = max(val[i - 1]
+ K[i - 1][w - wt[i - 1]],
K[i - 1][w])
else:
K[i][w] = K[i - 1][w]
res = K[n][W]
print(res)
w = W
for i in range(n, 0, -1):
if res <= 0:
break
if res == K[i - 1][w]:
continue
else:
print(wt[i - 1])
res = res - val[i - 1]
w = w - wt[i - 1]
val = [ 60, 100, 120 ]
wt = [ 10, 20, 30 ]
W = 50
n = len(val)
printknapSack(W, wt, val, n)
|
C#
using System ;
class GFG {
static int max(int a, int b)
{
return (a > b) ? a : b;
}
static void printknapSack(int W, int []wt,
int []val, int n)
{
int i, w;
int [,]K = new int[n + 1,W + 1];
for (i = 0; i <= n; i++) {
for (w = 0; w <= W; w++) {
if (i == 0 || w == 0)
K[i,w] = 0;
else if (wt[i - 1] <= w)
K[i,w] = Math.Max(val[i - 1] +
K[i - 1,w - wt[i - 1]], K[i - 1,w]);
else
K[i,w] = K[i - 1,w];
}
}
int res = K[n,W];
Console.WriteLine(res);
w = W;
for (i = n; i > 0 && res > 0; i--) {
if (res == K[i - 1,w])
continue;
else {
Console.Write(wt[i - 1] + " ");
res = res - val[i - 1];
w = w - wt[i - 1];
}
}
}
public static void Main()
{
int []val = { 60, 100, 120 };
int []wt = { 10, 20, 30 };
int W = 50;
int n = val.Length;
printknapSack(W, wt, val, n);
}
}
|
PHP
<?php
function printknapSack($W, &$wt, &$val, $n)
{
$K = array_fill(0, $n + 1,
array_fill(0, $W + 1, NULL));
for ($i = 0; $i <= $n; $i++)
{
for ($w = 0; $w <= $W; $w++)
{
if ($i == 0 || $w == 0)
$K[$i][$w] = 0;
else if ($wt[$i - 1] <= $w)
$K[$i][$w] = max($val[$i - 1] +
$K[$i - 1][$w - $wt[$i - 1]],
$K[$i - 1][$w]);
else
$K[$i][$w] = $K[$i - 1][$w];
}
}
$res = $K[$n][$W];
echo $res . "\n";
$w = $W;
for ($i = $n; $i > 0 && $res > 0; $i--)
{
if ($res == $K[$i - 1][$w])
continue;
else
{
echo $wt[$i - 1] . " ";
$res = $res - $val[$i - 1];
$w = $w - $wt[$i - 1];
}
}
}
$val = array(60, 100, 120);
$wt = array(10, 20, 30);
$W = 50;
$n = sizeof($val);
printknapSack($W, $wt, $val, $n);
?>
|
Javascript
<script>
function max(a,b)
{
return (a > b) ? a : b;
}
function printknapSack(W,wt,val,n)
{
let i, w;
let K = new Array(n + 1);
for( i=0;i<K.length;i++)
{
K[i]=new Array(W+1);
for(let j=0;j<W+1;j++)
{
K[i][j]=0;
}
}
for (i = 0; i <= n; i++) {
for (w = 0; w <= W; w++) {
if (i == 0 || w == 0)
K[i][w] = 0;
else if (wt[i - 1] <= w)
K[i][w] = Math.max(val[i - 1] +
K[i - 1][w - wt[i - 1]],
K[i - 1][w]);
else
K[i][w] = K[i - 1][w];
}
}
let res = K[n][W];
document.write(res+"<br>");
w = W;
for (i = n; i > 0 && res > 0; i--)
{
if (res == K[i - 1][w])
continue;
else {
document.write(wt[i - 1] + " ");
res = res - val[i - 1];
w = w - wt[i - 1];
}
}
}
let val=[60, 100, 120 ];
let wt=[10, 20, 30 ];
let W = 50;
let n = val.length;
printknapSack(W, wt, val, n);
</script>
|
Time complexity: O(n*W)
Space complexity: O(n*W)
Share your thoughts in the comments
Please Login to comment...