Largest number with maximum trailing nines which is less than N and greater than N-D

Given two numbers N and D. The task is to find out the largest number smaller than or equal to N which contains the maximum number of trailing nines and the difference between N and the number should not be greater than D. 
Examples:

Input: N = 1029, D = 102
Output: 999
1029 has 1 trailing nine while 999 has three 
trailing nine. Also 1029-999 = 30(which is less than 102).

Input: N = 10281, D = 1
Output: 10281

A naive approach will be to iterate from N till N-D and find the number with the largest number of trailing nines. 
An efficient approach can be found by some key observations. One key observation for this problem is that the largest number smaller than N ending with at least say(K) nines is 

[n – (n MOD 10^k) – 1]

Traverse all possible values of k starting from total no of digits of N to 1, and check whether d > n%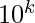. If no such value is obtained, the final answer will be N itself. Otherwise, check for the answer using the above observation.
Below is the implementation of the above approach. 

C++

// CPP to implement above function
#include <bits/stdc++.h>
using namespace std;

// It's better to use long long
// to handle big integers
#define ll long long

// function to count no of digits
ll dig(ll a)
{
    ll count = 0;
    while (a > 0) {
        a /= 10;
        count++;
    }
    return count;
}

// function to implement above approach
void required_number(ll num, ll n, ll d)
{
    ll i, j, power, a, flag = 0;
    for (i = num; i >= 1; i--) {
        power = pow(10, i);
        a = n % power;

        // if difference between power
        // and n doesn't exceed d
        if (d > a) {
            flag = 1;
            break;
        }
    }
    if (flag) {
        ll t = 0;

        // loop to build a number from the
        // appropriate no of digits containing only 9
        for (j = 0; j < i; j++) {
            t += 9 * pow(10, j);
        }

        // if the build number is
        // same as original number(n)
        if (n % power == t)
            cout << n;
        else {

            // observation
            cout << n - (n % power) - 1;
        }
    }
    else
        cout << n;
}

// Driver Code
int main()
{
    ll n = 1029, d = 102;

    // variable that stores no of digits in n
    ll num = dig(n);
    required_number(num, n, d);
    return 0;
}

Java

// Java code to implement above function
import java.io.*;

class GFG {

// It's better to use long
// to handle big integers
// function to count no. of digits
static long dig(long a)
{
    long count = 0;
    while (a > 0)
    {
        a /= 10;
        count++;
    }
    return count;
}

// function to implement above approach
 static void required_number(long num, long n, long d)
{
    long i, j, power=1, a, flag = 0;
    for (i = num; i >= 1; i--)
    {
        power = (long)Math.pow(10, i);
        a = n % power;

        // if difference between power
        // and n doesn't exceed d
        if (d > a)
        {
            flag = 1;
            break;
        }
    }

    if (flag>0)
    {
        long t = 0;

        // loop to build a number from the
        // appropriate no of digits containing
        // only 9
        for (j = 0; j < i; j++)
        {
            t += 9 * Math.pow(10, j);
        }

        // if the build number is
        // same as original number(n)
        if (n % power == t)
            System.out.print( n);

        else {

            // observation
            System.out.print( n - (n % power) - 1);
        }
    }
    else
        System.out.print(n);
}

    // Driver Code
    public static void main (String[] args)
    {
        long n = 1029, d = 102;

        // variable that stores no
        // of digits in n
        long num = dig(n);
        required_number(num, n, d);
    }
}

// This code is contributed by chandan_jnu

Python3

# Python3 to implement above function

# function to count no of digits
def dig(a):
    count = 0;
    while (a > 0):
        a /= 10
        count+=1
    return count


# function to implement above approach
def required_number(num, n, d):
    flag = 0
    power=0
    a=0
    for i in range(num,0,-1):
        power = pow(10, i)
        a = n % power

        # if difference between power
        # and n doesn't exceed d

        if (d > a):
            flag = 1
            break
    if(flag):
        t=0
        # loop to build a number from the
        # appropriate no of digits containing only 9
        for j in range(0,i):
            t += 9 * pow(10, j)

        # if the build number is
        # same as original number(n)
        if(n % power ==t):
            print(n,end="")
        else:
            # observation
            print((n - (n % power) - 1),end="")
    else:
        print(n,end="")
# Driver Code

if __name__ == "__main__":
    n = 1029
    d = 102

# variable that stores no of digits in n
    num = dig(n)
    required_number(num, n, d)

# this code is contributed by mits

C#

// C# code to implement
// above function
using System;

class GFG
{

// It's better to use long
// to handle big integers
// function to count no. of digits
static long dig(long a)
{
    long count = 0;
    while (a > 0)
    {
        a /= 10;
        count++;
    }
    return count;
}

// function to implement
// above approach
static void required_number(long num,
                            long n,
                            long d)
{
    long i, j, power = 1, a, flag = 0;
    for (i = num; i >= 1; i--)
    {
        power = (long)Math.Pow(10, i);
        a = n % power;

        // if difference between power
        // and n doesn't exceed d
        if (d > a)
        {
            flag = 1;
            break;
        }
    }

    if (flag > 0)
    {
        long t = 0;

        // loop to build a number
        // from the appropriate no
        // of digits containing only 9
        for (j = 0; j < i; j++)
        {
            t += (long)(9 * Math.Pow(10, j));
        }

        // if the build number is
        // same as original number(n)
        if (n % power == t)
            Console.Write( n);

        else
        {

            // observation
            Console.Write(n - (n % power) - 1);
        }
    }
    else
        Console.Write(n);
}

    // Driver Code
    public static void Main()
    {
        long n = 1029, d = 102;

        // variable that stores
        // no. of digits in n
        long num = dig(n);
        required_number(num, n, d);
    }
}

// This code is contributed
// by chandan_jnu

PHP

<?php
// PHP to implement above function

// function to count no of digits
function dig($a)
{
    $count = 0;
    while ($a > 0)
    {
        $a = (int)($a / 10);
        $count++;
    }
    return $count;
}

// function to implement above approach
function required_number($num, $n, $d)
{
    $flag = 0;
    for ($i = $num; $i >= 1; $i--)
    {
        $power = pow(10, $i);
        $a = $n % $power;

        // if difference between power
        // and n doesn't exceed d
        if ($d > $a)
        {
            $flag = 1;
            break;
        }
    }
    if ($flag)
    {
        $t = 0;

        // loop to build a number from the
        // appropriate no of digits containing only 9
        for ($j = 0; $j < $i; $j++)
        {
            $t += 9 * pow(10, $j);
        }

        // if the build number is
        // same as original number(n)
        if ($n % $power == $t)
            echo $n;
        else
        {

            // observation
            echo ($n - ($n % $power) - 1);
        }
    }
    else
        echo $n;
}

// Driver Code
$n = 1029;
$d = 102;

// variable that stores no of
// digits in n
$num = dig($n);
required_number($num, $n, $d);

// This code is contributed by mits
?>

Javascript

<script>

// javascript code to implement above function

// It's better to use var
// to handle big integers
// function to count no. of digits
function dig(a)
{
    var count = 0;
    while (a > 0)
    {
        a /= 10;
        count++;
    }
    return count;
}

// function to implement above approach
 function required_number(num , n , d)
{
    var i, j, power=1, a, flag = 0;
    for (i = num; i >= 1; i--)
    {
        power = Math.pow(10, i);
        a = n % power;

        // if difference between power
        // and n doesn't exceed d
        if (d > a)
        {
            flag = 1;
            break;
        }
    }

    if (flag>0)
    {
        var t = 0;

        // loop to build a number from the
        // appropriate no of digits containing
        // only 9
        for (j = 0; j < i; j++)
        {
            t += 9 * Math.pow(10, j);
        }

        // if the build number is
        // same as original number(n)
        if (n % power == t)
            document.write( n);

        else {

            // observation
            document.write( n - (n % power) - 1);
        }
    }
    else
        document.write(n);
}

    // Driver Code
 var n = 1029, d = 102;

 // variable that stores no
 // of digits in n
 var num = dig(n);
 required_number(num, n, d);

// This code is contributed by 29AjayKumar
</script>

Output:

999

Time Complexity: O(logn)
Auxiliary Space: O(1)

Another Approach: The approach is to reduce n by variable num that is 9 99 999 and so on and divide it by temp which is 1 10 100 1000 and so on. If at any point n is less than num we break and return the ans. For each iteration we calculate a value x as (n-num)/temp then if (x*temp)+ num is greater than equal to (n-d) this will be our ans with most number of nines as basically we are reducing n by a factor and adding num (the most number of 9s possible) as it is of the form 9 99 999 and so on.

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>
using namespace std;

int maxPossible9s(int n, int d)
{
    // initialising temp and ans variable to 1
    int temp = 1;
    int ans = 1;
    int num = 0;
    // taking a condition which always holds true
    while (true) {
        // condition to break
        if (n < num) {
            break;
        }
        else {
            // x is a factor by which we can calculate the
            // most number of 9s and then adding the most
            // number of 9s
            int x = (n - num) / temp;
            // if the condition is true then our ans will be
            // the value (x * temp + num) because num is of
            // the format 9 99 999 so on and hence gives the
            // most number of 9s
            if (x * temp + num >= (n - d)) {
                ans = x * temp + num;
            }
            // temp will be of the format 1 10 100 1000
            // 10000 and so on
            temp *= 10;
            // num will be of the format 9 99 999 9999 and
            // so on
            num = num * 10 + 9;
        }
    }
    return ans;
}

int main()
{
    int n = 1029;
    int d = 102;

    cout << maxPossible9s(n, d) << endl;
}

Java

/*package whatever //do not write package name here */

import java.io.*;

class GFG {
  static int maxPossible9s(int n, int d)
  {

    // initialising temp and ans variable to 1
    int temp = 1;
    int ans = 1;
    int num = 0;

    // taking a condition which always holds true
    while (true) {
      // condition to break
      if (n < num) {
        break;
      }
      else
      {

        // x is a factor by which we can calculate the
        // most number of 9s and then adding the most
        // number of 9s
        int x = (n - num) / temp;

        // if the condition is true then our ans will be
        // the value (x * temp + num) because num is of
        // the format 9 99 999 so on and hence gives the
        // most number of 9s
        if (x * temp + num >= (n - d)) {
          ans = x * temp + num;
        }

        // temp will be of the format 1 10 100 1000
        // 10000 and so on
        temp *= 10;

        // num will be of the format 9 99 999 9999 and
        // so on
        num = num * 10 + 9;
      }
    }
    return ans;
  }

  // Driver code
  public static void main(String args[])
  {
    int n = 1029;
    int d = 102;

    System.out.println(maxPossible9s(n, d));
  }
}

// This code is contributed by shinjanpatra.

Python3

def maxPossible9s(n, d):

    # initialising temp and ans variable to 1
    temp = 1
    ans = 1
    num = 0

    # taking a condition which always holds true
    while (True):

        # condition to break
        if (n < num):
            break

        else:
            # x is a factor by which we can calculate the
            # most number of 9s and then adding the most
            # number of 9s
            x = (n - num) // temp

            # if the condition is true then our ans will be
            # the value (x * temp + num) because num is of
            # the format 9 99 999 so on and hence gives the
            # most number of 9s
            if (x * temp + num >= (n - d)):
                ans = x * temp + num

            # temp will be of the format 1 10 100 1000
            # 10000 and so on
            temp *= 10

            # num will be of the format 9 99 999 9999 and
            # so on
            num = num * 10 + 9

    return ans

# driver code

n = 1029
d = 102

print(maxPossible9s(n, d))

# This code is contributed by shinjanpatra

C#

// C# code to implement above approach
using System;

class GFG
{
   static int maxPossible9s(int n, int d)
  {

    // initialising temp and ans variable to 1
    int temp = 1;
    int ans = 1;
    int num = 0;

    // taking a condition which always holds true
    while (true) {
      // condition to break
      if (n < num) {
        break;
      }
      else
      {

        // x is a factor by which we can calculate the
        // most number of 9s and then adding the most
        // number of 9s
        int x = (n - num) / temp;

        // if the condition is true then our ans will be
        // the value (x * temp + num) because num is of
        // the format 9 99 999 so on and hence gives the
        // most number of 9s
        if (x * temp + num >= (n - d)) {
          ans = x * temp + num;
        }

        // temp will be of the format 1 10 100 1000
        // 10000 and so on
        temp *= 10;

        // num will be of the format 9 99 999 9999 and
        // so on
        num = num * 10 + 9;
      }
    }
    return ans;
  }

    // Driver Code
    public static void Main()
    {
        int n = 1029;
        int d = 102;

        Console.Write(maxPossible9s(n, d));
    }
}

// This code is contributed by Pushpesh Raj.

Javascript

<script>

function maxPossible9s(n, d)
{
    // initialising temp and ans variable to 1
    let temp = 1;
    let ans = 1;
    let num = 0;
    // taking a condition which always holds true
    while (true) {
        // condition to break
        if (n < num) {
            break;
        }
        else {
            // x is a factor by which we can calculate the
            // most number of 9s and then adding the most
            // number of 9s
            let x = Math.floor((n - num) / temp);
            // if the condition is true then our ans will be
            // the value (x * temp + num) because num is of
            // the format 9 99 999 so on and hence gives the
            // most number of 9s
            if (x * temp + num >= (n - d)) {
                ans = x * temp + num;
            }
            // temp will be of the format 1 10 100 1000
            // 10000 and so on
            temp *= 10;
            // num will be of the format 9 99 999 9999 and
            // so on
            num = num * 10 + 9;
        }
    }
    return ans;
}

// driver code

let n = 1029;
let d = 102;

document.write(maxPossible9s(n, d),"</br>");

// code is contributed by shinjanpatra

</script>

 Output:

999

Time Complexity: O(logn)
Auxiliary Space: O(1), as no extra space is used