Print the longest path from root to leaf in a Binary tree

Given a binary tree, the task is to print the longest path from the root node to the leaf node. If there are multiple answers print any one of them.

Examples:

Input: 
      4
     / \
    3   6
       / \
      5   7
Output: 
4 -> 6 -> 7 
Explanation:
Longest paths from root to leaf
are (4 -> 6 -> 5) 
and (4 -> 6 -> 7).
Print any of them.

Input:
         1
        / \
       2   3
     /  \
    4    5
          \
           6
Output:
1 -> 2 -> 5 -> 6

Naive Approach: The idea is to generate all possible paths from the root node to all leaf nodes, keep track of the path with maximum length, finally print the longest path.

Time Complexity: O(N²)

Efficient Approach: The idea is to use Recursion to solve this problem efficiently. The main idea is to recursively get the longest path from the left subtree and right subtree then add the current node to one which has a greater length and it will be the longest path from the current node to leaf. Starting with the root node, follow the steps below for each node called recursively.

If the root node is null then no path exists, return an empty vector.
Get the longest path from right subtree in a vector rightvect by recursively traversing root -> right.
Similarly, get the longest path from left subtree in a vector leftvect by recursively traversing root -> left.
Compare the length of rightvect and leftvect and append the current node to the longer of the two and return that vector.

By following the above steps, the vector obtained at the end of the tree traversal is the longest path possible. Print the vector in reverse as the longest path from the root to leaf.

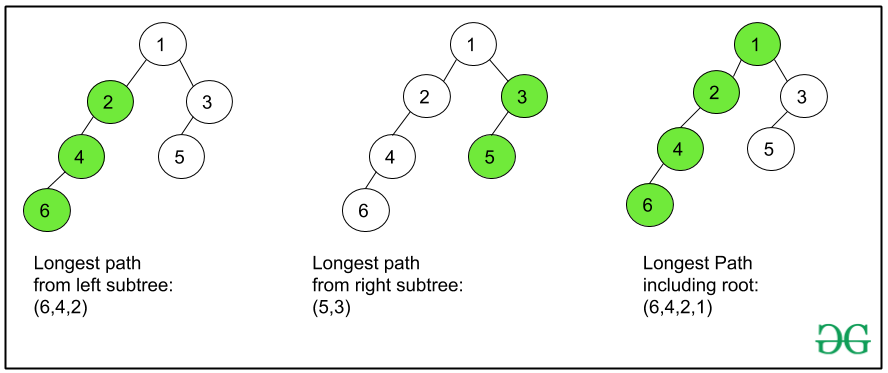
Look at this image to understand how the longest paths from the nodes of left and right subtree are used to obtain the longest path from the current node:

Below is the implementation of the above approach:

C++

// C++ Program to print Longest Path
// from root to leaf in a Binary tree
#include <bits/stdc++.h>
using namespace std;
 
// Tree node Structure
struct Node {
    int data;
    Node *left, *right;
};
 
struct Node* newNode(int data)
{
    struct Node* node = new Node;
    node->data = data;
    node->left = node->right = NULL;
 
    return (node);
}
 
// Function to find and return the
// longest path
vector<int> longestPath(Node* root)
{
 
    // If root is null means there
    // is no binary tree so
    // return a empty vector
    if (root == NULL) {
        vector<int> temp
            = {};
        return temp;
    }
 
    // Recursive call on root->right
    vector<int> rightvect
        = longestPath(root->right);
 
    // Recursive call on root->left
    vector<int> leftvect
        = longestPath(root->left);
 
    // Compare the size of the two vectors
    // and insert current node accordingly
    if (leftvect.size() > rightvect.size())
        leftvect.push_back(root->data);
 
    else
        rightvect.push_back(root->data);
 
    // Return the appropriate vector
    return (leftvect.size() > rightvect.size()
                ? leftvect
                : rightvect);
}
 
// Driver Code
int main()
{
    struct Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    root->left->right->right = newNode(6);
 
    vector<int> output = longestPath(root);
    int n = output.size();
 
    cout << output[n - 1];
    for (int i = n - 2; i >= 0; i--) {
        cout << " -> " << output[i];
    }
 
    return 0;
}

Java

// Java program to print Longest Path
// from root to leaf in a Binary tree
import java.io.*;
import java.util.ArrayList;
 
class GFG{
     
// Binary tree node
static class Node
{
    Node left;
    Node right;
    int data;
};
 
// Function to create a new
// Binary node
static Node newNode(int data)
{
    Node temp = new Node();
 
    temp.data = data;
    temp.left = null;
    temp.right = null;
 
    return temp;
}
 
// Function to find and return the
// longest path
public static ArrayList<Integer> longestPath(Node root)
{
     
    // If root is null means there
    // is no binary tree so
    // return a empty vector
    if(root == null)
    {
        ArrayList<Integer> output = new ArrayList<>();
        return output;
    }
     
    // Recursive call on root.right
    ArrayList<Integer> right = longestPath(root.right);
     
    // Recursive call on root.left
    ArrayList<Integer> left = longestPath(root.left);
     
    // Compare the size of the two ArrayList
    // and insert current node accordingly
    if(right.size() < left.size())
    {
        left.add(root.data);
    }
    else
    {
        right.add(root.data);
    }
     
    // Return the appropriate ArrayList
    return (left.size() >
            right.size() ? left :right);
}
 
// Driver Code
public static void main(String[] args)
{
    Node root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(4);
    root.left.right = newNode(5);
    root.left.right.right = newNode(6);
     
    ArrayList<Integer> output = longestPath(root);
    int n = output.size();
     
    System.out.print(output.get(n - 1));
    for(int i = n - 2; i >= 0; i--)
    {
        System.out.print(" -> " + output.get(i));
    }
}
}
 
// This code is contributed by HamreetSingh

Python3

# Python3 program to print longest path
# from root to leaf in a Binary tree
 
# Tree node Structure
class Node:
     
    def __init__(self, key):
         
        self.data = key
        self.left = None
        self.right = None
         
# Function to find and return the
# longest path
def longestPath(root):
     
    # If root is null means there
    # is no binary tree so
    # return a empty vector
    if (root == None):
        return []
 
    # Recursive call on root.right
    rightvect = longestPath(root.right)
 
    # Recursive call on root.left
    leftvect = longestPath(root.left)
 
    # Compare the size of the two vectors
    # and insert current node accordingly
    if (len(leftvect) > len(rightvect)):
        leftvect.append(root.data)
    else:
        rightvect.append(root.data)
 
    # Return the appropriate vector
    if len(leftvect) > len(rightvect):
        return leftvect
 
    return rightvect
 
# Driver Code
if __name__ == '__main__':
     
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)
    root.left.right.right = Node(6)
 
    output = longestPath(root)
    n = len(output)
 
    print(output[n - 1], end = "")
    for i in range(n - 2, -1, -1):
        print(" ->", output[i], end = "")
 
# This code is contributed by mohit kumar 29

C#

// C# program to print
// longest Path from
// root to leaf in a
// Binary tree
using System;
using System.Collections.Generic;
class GFG{
     
// Binary tree node
class Node
{
  public Node left;
  public Node right;
  public int data;
};
 
// Function to create a new
// Binary node
static Node newNode(int data)
{
  Node temp = new Node();
  temp.data = data;
  temp.left = null;
  temp.right = null;
  return temp;
}
 
// Function to find and
// return the longest path
static List<int> longestPath(Node root)
{   
  // If root is null means there
  // is no binary tree so
  // return a empty vector
  if(root == null)
  {
    List<int> output = new List<int>();
    return output;
  }
 
  // Recursive call on root.right
  List<int> right = longestPath(root.right);
 
  // Recursive call on root.left
  List<int> left = longestPath(root.left);
 
  // Compare the size of the two List
  // and insert current node accordingly
  if(right.Count < left.Count)
  {
    left.Add(root.data);
  }
  else
  {
    right.Add(root.data);
  }
 
  // Return the appropriate List
  return (left.Count >
          right.Count ?
          left :right);
}
 
// Driver Code
public static void Main(String[] args)
{
  Node root = newNode(1);
  root.left = newNode(2);
  root.right = newNode(3);
  root.left.left = newNode(4);
  root.left.right = newNode(5);
  root.left.right.right = newNode(6);
 
  List<int> output = longestPath(root);
  int n = output.Count;
 
  Console.Write(output[n - 1]);
  for(int i = n - 2; i >= 0; i--)
  {
    Console.Write(" -> " + output[i]);
  }
}
}
 
// This code is contributed by 29AjayKumar

Javascript

<script>
 
// Javascript program to print Longest Path
// from root to leaf in a Binary tree
 
// Binary tree node
class Node
{
     
    // Function to create a new
    // Binary node
    constructor(data)
    {
        this.data = data;
        this.left = this.right = null;
    }
}
 
// Function to find and return the
// longest path
function longestPath(root)
{
     
    // If root is null means there
    // is no binary tree so
    // return a empty vector
    if (root == null)
    {
        let output = [];
        return output;
    }
      
    // Recursive call on root.right
    let right = longestPath(root.right);
      
    // Recursive call on root.left
    let left = longestPath(root.left);
      
    // Compare the size of the two ArrayList
    // and insert current node accordingly
    if (right.length < left.length)
    {
        left.push(root.data);
    }
    else
    {
        right.push(root.data);
    }
      
    // Return the appropriate ArrayList
    return (left.length >
            right.length ? left :right);
}
 
// Driver code
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.left.right.right = new Node(6);
 
let output = longestPath(root);
let n = output.length;
 
document.write(output[n - 1]);
for(let i = n - 2; i >= 0; i--)
{
    document.write(" -> " + output[i]);
}
 
// This code is contributed by unknown2108
 
</script>