Print path from root to all nodes in a Complete Binary Tree
Last Updated :
10 Jan, 2023
Given a number N which is the total number of nodes in a complete binary tree where nodes are number from 1 to N sequentially level-wise. The task is to write a program to print paths from root to all of the nodes in the Complete Binary Tree.
For N = 3, the tree will be:
1
/ \
2 3
For N = 7, the tree will be:
1
/ \
2 3
/ \ / \
4 5 6 7
Examples:
Input : 7
Output :
1
1 2
1 2 4
1 2 5
1 3
1 3 6
1 3 7
Input : 4
Output :
1
1 2
1 2 4
1 3
Explanation:- Since, the given tree is a complete binary tree. For every node 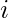 we can calculate its left child as 2*i and right child as 2*i + 1.
we can calculate its left child as 2*i and right child as 2*i + 1.
The idea is to use a backtracking approach to print all paths. Maintain a vector to store paths, initially push the root node 1 to it, and before pushing the left and right children print the current path stored in it and then call the function for the left and right children as well.
Below is the complete implementation of the above approach:
C++
#include <iostream>
#include <vector>
using namespace std;
void printPath(vector<int> res, int nThNode, int kThNode)
{
if (kThNode > nThNode)
return;
res.push_back(kThNode);
for (int i = 0; i < res.size(); i++)
cout << res[i] << " ";
cout << "\n";
printPath(res, nThNode, kThNode * 2);
printPath(res, nThNode, kThNode * 2 + 1);
}
void printPathToCoverAllNodeUtil(int nThNode)
{
vector<int> res;
printPath(res, nThNode, 1);
}
int main()
{
int nThNode = 7;
printPathToCoverAllNodeUtil(nThNode);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void printPath(Vector<Integer> res,
int nThNode, int kThNode)
{
if (kThNode > nThNode)
return;
res.add(kThNode);
for (int i = 0; i < res.size(); i++)
System.out.print( res.get(i) + " ");
System.out.print( "\n");
printPath(res, nThNode, kThNode * 2);
printPath(res, nThNode, kThNode * 2 + 1);
res.remove(res.size()-1);
}
static void printPathToCoverAllNodeUtil(int nThNode)
{
Vector<Integer> res=new Vector<Integer>();
printPath(res, nThNode, 1);
}
public static void main(String args[])
{
int nThNode = 7;
printPathToCoverAllNodeUtil(nThNode);
}
}
|
Python3
def printPath(res, nThNode, kThNode):
if kThNode > nThNode:
return
res.append(kThNode)
for i in range(0, len(res)):
print(res[i], end = " ")
print()
printPath(res[:], nThNode, kThNode * 2)
printPath(res[:], nThNode, kThNode * 2 + 1)
def printPathToCoverAllNodeUtil(nThNode):
res = []
printPath(res, nThNode, 1)
if __name__ == "__main__":
nThNode = 7
printPathToCoverAllNodeUtil(nThNode)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static void printPath(List<int> res,
int nThNode, int kThNode)
{
if (kThNode > nThNode)
return;
res.Add(kThNode);
for (int i = 0; i < res.Count; i++)
Console.Write( res[i] + " ");
Console.Write( "\n");
printPath(res, nThNode, kThNode * 2);
printPath(res, nThNode, kThNode * 2 + 1);
res.RemoveAt(res.Count-1);
}
static void printPathToCoverAllNodeUtil(int nThNode)
{
List<int> res=new List<int>();
printPath(res, nThNode, 1);
}
public static void Main(String []args)
{
int nThNode = 7;
printPathToCoverAllNodeUtil(nThNode);
}
}
|
PHP
<?php
function printPath($res, $nThNode, $kThNode)
{
if ($kThNode > $nThNode)
return;
array_push($res, $kThNode);
for ($i = 0; $i < count($res); $i++)
echo $res[$i] . " ";
echo "\n";
printPath($res, $nThNode, $kThNode * 2);
printPath($res, $nThNode, $kThNode * 2 + 1);
}
function printPathToCoverAllNodeUtil($nThNode)
{
$res = array();
printPath($res, $nThNode, 1);
}
$nThNode = 7;
printPathToCoverAllNodeUtil($nThNode);
?>
|
Javascript
<script>
function printPath(res, nThNode, kThNode)
{
if (kThNode > nThNode)
return;
res.push(kThNode);
for (var i = 0; i < res.length; i++)
document.write( res[i] + " ");
document.write( "<br>");
printPath(res, nThNode, kThNode * 2);
printPath(res, nThNode, kThNode * 2 + 1);
res.pop()
}
function printPathToCoverAllNodeUtil( nThNode)
{
var res = [];
printPath(res, nThNode, 1);
}
var nThNode = 7;
printPathToCoverAllNodeUtil(nThNode);
</script>
|
Output: 1
1 2
1 2 4
1 2 5
1 3
1 3 6
1 3 7
Time Complexity: O(N*H) where N is the number of nodes and H is the height of binary tree.
Auxiliary Space: O(H) where H is the height of binary tree.
Share your thoughts in the comments
Please Login to comment...