Print Nodes which are not part of any cycle in a Directed Graph
Last Updated :
14 Apr, 2023
Given a directed graph G N nodes and E Edges consisting of nodes valued [0, N – 1] and a 2D array Edges[][2] of type {u, v} that denotes a directed edge between vertices u and v. The task is to find the nodes that are not part of any cycle in the given graph G.
Examples:
Input: N = 4, E = 4, Edges[][2] = { {0, 2}, {0, 1}, {2, 3}, {3, 0} }
Output: 1
Explanation:
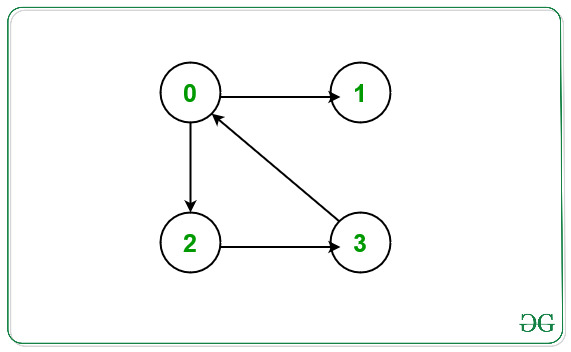
From the given graph above there exists a cycle between the nodes 0 -> 2 -> 3 -> 0.
Node which doesn’t occurs in any cycle is 1.
Hence, print 1.
Input: N = 6, E = 7, Edges[][2] = { {0, 1}, {0, 2}, {1, 3}, {2, 1}, {2, 5}, {3, 0}, {4, 5}}
Output: 4 5
Explanation:
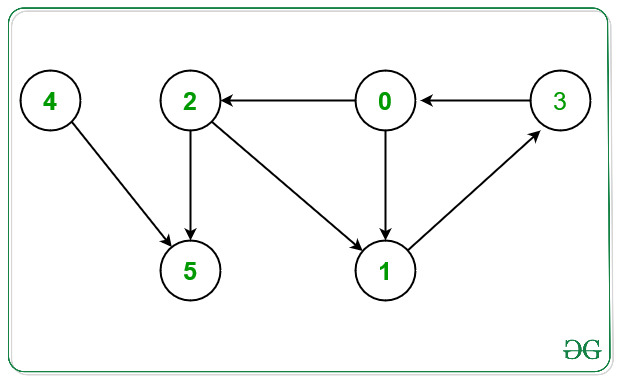
From the given graph above there exists a cycle between the nodes:
1) 0 -> 1 -> 3 -> 0.
2) 0 -> 2 -> 1 -> 3 -> 0.
Nodes which doesn’t occurs in any cycle are 4 and 5.
Hence, print 4 and 5.
Naive Approach: The simplest approach is to detect a cycle in a directed graph for each node in the given graph and print only those nodes that are not a part of any cycle in the given graph.
Time Complexity: O(V * (V + E)), where V is the number of vertices and E is the number of edges.
Auxiliary Space: O(V)
Efficient Approach: To optimize the above approach, the idea is to store the intermediate node as a visited cycle node whenever any cycle in the given graph. To implement this part use an auxiliary array cyclePart[] that will store the intermediate cycle node while performing the DFS Traversal. Below are the steps:
- Initialize an auxiliary array cyclePart[] of size N, such that if cyclePart[i] = 0, then ith node doesn’t exist in any cycle.
- Initialize an auxiliary array recStack[] of size N, such that it will store the visited node in the recursion stack by marking that node as true.
- Perform the DFS Traversal on the given graph for each unvisited node and do the following:
- Now find a cycle in the given graph, whenever a cycle is found, mark the node in cyclePart[] as true as this node is a part of the cycle.
- If any node is visited in the recursive call and is recStack[node] is also true then that node is a part of the cycle then mark that node as true.
- After performing the DFS Traversal, traverse the array cyclePart[] and print all those nodes that are marked as false as these nodes are not the part of any cycle.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class Graph {
int V;
list<int>* adj;
bool printNodesNotInCycleUtil(
int v, bool visited[], bool* rs,
bool* cyclePart);
public:
Graph(int V);
void addEdge(int v, int w);
void printNodesNotInCycle();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
}
bool Graph::printNodesNotInCycleUtil(
int v, bool visited[],
bool* recStack, bool* cyclePart)
{
if (visited[v] == false) {
visited[v] = true;
recStack[v] = true;
for (auto& child : adj[v]) {
if (!visited[child]
&& printNodesNotInCycleUtil(
child, visited,
recStack, cyclePart)) {
cyclePart[child] = 1;
return true;
}
else if (recStack[child]) {
cyclePart[child] = 1;
return true;
}
}
}
recStack[v] = false;
return false;
}
void Graph::printNodesNotInCycle()
{
bool* visited = new bool[V];
bool* recStack = new bool[V];
bool* cyclePart = new bool[V];
for (int i = 0; i < V; i++) {
visited[i] = false;
recStack[i] = false;
cyclePart[i] = false;
}
for (int i = 0; i < V; i++) {
if (!visited[i]) {
if (printNodesNotInCycleUtil(
i, visited, recStack,
cyclePart)) {
cyclePart[i] = 1;
}
}
}
for (int i = 0; i < V; i++) {
if (cyclePart[i] == 0) {
cout << i << " ";
}
}
}
void solve(int N, int E,
int Edges[][2])
{
Graph g(N);
for (int i = 0; i < E; i++) {
g.addEdge(Edges[i][0],
Edges[i][1]);
}
g.printNodesNotInCycle();
}
int main()
{
int N = 6;
int E = 7;
int Edges[][2] = { { 0, 1 }, { 0, 2 },
{ 1, 3 }, { 2, 1 },
{ 2, 5 }, { 3, 0 },
{ 4, 5 } };
solve(N, E, Edges);
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
class GFG
{
static ArrayList<ArrayList<Integer>> adj;
static int V;
static boolean printNodesNotInCycleUtil(
int v, boolean visited[],
boolean[] recStack, boolean[] cyclePart)
{
if (visited[v] == false)
{
visited[v] = true;
recStack[v] = true;
for (Integer child : adj.get(v))
{
if (!visited[child]
&& printNodesNotInCycleUtil(
child, visited,
recStack, cyclePart))
{
cyclePart[child] = true;
return true;
}
else if (recStack[child])
{
cyclePart[child] = true;
return true;
}
}
}
recStack[v] = false;
return false;
}
static void printNodesNotInCycle()
{
boolean[] visited = new boolean[V];
boolean[] recStack = new boolean[V];
boolean[] cyclePart = new boolean[V];
for (int i = 0; i < V; i++)
{
if (!visited[i])
{
if (printNodesNotInCycleUtil(
i, visited, recStack,
cyclePart)) {
cyclePart[i] = true;
}
}
}
for (int i = 0; i < V; i++)
{
if (!cyclePart[i])
{
System.out.print(i+" ");
}
}
}
static void solve(int N, int E,
int Edges[][])
{
adj = new ArrayList<>();
for(int i = 0; i < N; i++)
adj.add(new ArrayList<>());
for (int i = 0; i < E; i++)
{
adj.get(Edges[i][0]).add(Edges[i][1]);
}
printNodesNotInCycle();
}
public static void main (String[] args)
{
V = 6;
int E = 7;
int Edges[][] = { { 0, 1 }, { 0, 2 },
{ 1, 3 }, { 2, 1 },
{ 2, 5 }, { 3, 0 },
{ 4, 5 } };
solve(V, E, Edges);
}
}
|
Python3
class Graph:
def __init__(self, V):
self.V = V
self.adj = [[] for i in range(self.V)]
def addEdge(self, v, w):
self.adj[v].append(w);
def printNodesNotInCycleUtil(self, v, visited,recStack, cyclePart):
if (visited[v] == False):
visited[v] = True;
recStack[v] = True;
for child in self.adj[v]:
if (not visited[child] and self.printNodesNotInCycleUtil(child, visited,recStack, cyclePart)):
cyclePart[child] = 1;
return True;
elif (recStack[child]):
cyclePart[child] = 1;
return True;
recStack[v] = False;
return False;
def printNodesNotInCycle(self):
visited = [False for i in range(self.V)];
recStack = [False for i in range(self.V)];
cyclePart = [False for i in range(self.V)]
for i in range(self.V):
if (not visited[i]):
if(self.printNodesNotInCycleUtil(
i, visited, recStack,
cyclePart)):
cyclePart[i] = 1;
for i in range(self.V):
if (cyclePart[i] == 0) :
print(i,end=' ')
def solve( N, E, Edges):
g = Graph(N);
for i in range(E):
g.addEdge(Edges[i][0],
Edges[i][1]);
g.printNodesNotInCycle();
if __name__=='__main__':
N = 6;
E = 7;
Edges = [ [ 0, 1 ], [ 0, 2 ],
[ 1, 3 ], [ 2, 1 ],
[ 2, 5 ], [ 3, 0 ],
[ 4, 5 ] ];
solve(N, E, Edges);
|
C#
using System;
using System.Collections.Generic;
public class GFG
{
static List<List<int>> adj;
static int V;
static bool printNodesNotInCycleUtil(
int v, bool []visited,
bool[] recStack, bool[] cyclePart)
{
if (visited[v] == false)
{
visited[v] = true;
recStack[v] = true;
foreach (int child in adj[v])
{
if (!visited[child]
&& printNodesNotInCycleUtil(
child, visited,
recStack, cyclePart))
{
cyclePart[child] = true;
return true;
}
else if (recStack[child])
{
cyclePart[child] = true;
return true;
}
}
}
recStack[v] = false;
return false;
}
static void printNodesNotInCycle()
{
bool[] visited = new bool[V];
bool[] recStack = new bool[V];
bool[] cyclePart = new bool[V];
for (int i = 0; i < V; i++)
{
if (!visited[i])
{
if (printNodesNotInCycleUtil(
i, visited, recStack,
cyclePart)) {
cyclePart[i] = true;
}
}
}
for (int i = 0; i < V; i++)
{
if (!cyclePart[i])
{
Console.Write(i+" ");
}
}
}
static void solve(int N, int E,
int [,]Edges)
{
adj = new List<List<int>>();
for(int i = 0; i < N; i++)
adj.Add(new List<int>());
for (int i = 0; i < E; i++)
{
adj[Edges[i,0]].Add(Edges[i,1]);
}
printNodesNotInCycle();
}
public static void Main(String[] args)
{
V = 6;
int E = 7;
int [,]Edges = { { 0, 1 }, { 0, 2 },
{ 1, 3 }, { 2, 1 },
{ 2, 5 }, { 3, 0 },
{ 4, 5 } };
solve(V, E, Edges);
}
}
|
Javascript
<script>
class Graph{
constructor(V){
this.V = V
this.adj = new Array(V).fill(0).map(()=>[])
}
addEdge(v, w){
this.adj[v].push(w);
}
printNodesNotInCycleUtil(v, visited,recStack, cyclePart){
if (visited[v] == false){
visited[v] = true;
recStack[v] = true;
for(let child of this.adj[v]){
if (visited[child] == false && this.printNodesNotInCycleUtil(child, visited,recStack, cyclePart)){
cyclePart[child] = 1;
return true;
}
else if (recStack[child]){
cyclePart[child] = 1;
return true;
}
}
}
recStack[v] = false;
return false;
}
printNodesNotInCycle(){
let visited = new Array(this.V).fill(false);
let recStack = new Array(this.V).fill(false);
let cyclePart = new Array(this.V).fill(false)
for(let i=0;i<this.V;i++){
if (visited[i] == false){
if(this.printNodesNotInCycleUtil(
i, visited, recStack,
cyclePart))
cyclePart[i] = 1;
}
}
for(let i=0;i<this.V;i++){
if (cyclePart[i] == 0)
document.write(i,' ')
}
}
}
function solve(N, E, Edges){
let g = new Graph(N);
for(let i=0;i<E;i++){
g.addEdge(Edges[i][0],
Edges[i][1]);
}
g.printNodesNotInCycle();
}
let N = 6;
let E = 7;
let Edges = [ [ 0, 1 ], [ 0, 2 ],
[ 1, 3 ], [ 2, 1 ],
[ 2, 5 ], [ 3, 0 ],
[ 4, 5 ] ];
solve(N, E, Edges)
</script>
|
Time Complexity: O(V + E)
Space Complexity: O(V)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...