Print Levels of all nodes in a Binary Tree
Last Updated :
03 Mar, 2023
Given a Binary Tree and a key, write a function that prints levels of all keys in given binary tree.
For example, consider the following tree. If the input key is 3, then your function should return 1. If the input key is 4, then your function should return 3. And for key which is not present in key, then your function should return 0.
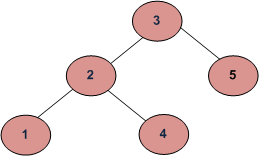
Input:
3
/ \
2 5
/ \
1 4
output:
Level of 1 is 3
Level of 2 is 2
Level of 3 is 1
Level of 4 is 3
Level of 5 is 2
We have discussed an recursive solution in below post.
Get Level of a node in a Binary Tree
In this post, an iterative solution based on Level order traversal is discussed. We store level of every node in queue together with the node while doing the traversal.
Algorithm:
Step 1: Start
Step 2: Create a class of static type name it as pair which have two parameter one of node type an danother is of integer type.
Step 3: create a function of static type with null return type nameas “printLevel” which take raaotof linked list as input.
a. Set base condition as if ( root == null ) return
b. Create a queue to hold the tree nodes and their levels name it as “q”.
c. add root node at level 1 in q
d. Define a pair variable p.
e. start a while loop to do level-order traversal until queue is empty:
1. Dequeue a node and its level into the pair variable p at the front of the queue.
2. Print the data and the node’s level
3. Enqueue the node’s left child with its level increased by 1 if it has one.
4. Enqueue the node’s right child with its level increased by 1 if it has one.
step 4: End
Implementation:
C++
Java
Python3
<div id="highlighter_959175" class="syntaxhighlighter nogutter "><table border="0" cellpadding="0" cellspacing="0"><tbody><tr><td class="code"><div class="container"><div class="line number1 index0 alt2"><code class="comments">
|
C#
using System;
using System.Collections.Generic;
public class Print_Level_Btree
{
public class Node
{
public int data;
public Node left;
public Node right;
public Node(int data)
{
this.data = data;
left = null;
right = null;
}
}
public class Pair
{
public Node n;
public int i;
public Pair(Node n, int i)
{
this.n = n;
this.i = i;
}
}
public static void printLevel(Node root)
{
if (root == null)
{
return;
}
LinkedList<Pair> q = new LinkedList<Pair>();
q.AddLast(new Pair(root, 1));
Pair p;
while (q.Count > 0)
{
p = q.First.Value;
q.RemoveFirst();
Console.WriteLine("Level of " + p.n.data + " is " + p.i);
if (p.n.left != null)
{
q.AddLast(new Pair(p.n.left, p.i + 1));
}
if (p.n.right != null)
{
q.AddLast(new Pair(p.n.right, p.i + 1));
}
}
}
public static void Main(string[] args)
{
Node root = null;
root = new Node(3);
root.left = new Node(2);
root.right = new Node(5);
root.left.left = new Node(1);
root.left.right = new Node(4);
printLevel(root);
}
}
|
Javascript
<script>
class Node
{
constructor(data) {
this.left = null;
this.right = null;
this.data = data;
}
}
function printLevel(root)
{
if (root == null)
return;
let q = [];
q.push([root, 1]);
let p;
while (q.length > 0) {
p = q[0];
q.shift();
document.write("Level of " + p[0].data +
" is " + p[1] + "</br>");
if (p[0].left != null)
q.push([p[0].left, p[1] + 1]);
if (p[0].right != null)
q.push([p[0].right, p[1] + 1]);
}
}
let root = null;
root = new Node(3);
root.left = new Node(2);
root.right = new Node(5);
root.left.left = new Node(1);
root.left.right = new Node(4);
printLevel(root);
</script>
|
Output
Level of 3 is 1
Level of 2 is 2
Level of 5 is 2
Level of 1 is 3
Level of 4 is 3
Time Complexity: O(n) where n is the number of nodes in the given Binary Tree.
Auxiliary Space: O(n) where n is the number of nodes in the given Binary tree due to queue data structure.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...