Print all unique combinations of setting N pieces on an NxN board
Last Updated :
06 Dec, 2021
Given an integer N, the task is to print all the unique combinations of putting N pieces in an NxN board.
Note: Print (“*”) for pieces and (“-“) for an empty space.
Example:
Input: N = 2
Output:
* *
– –
* –
* –
* –
– *
– *
* –
– *
– *
– –
* *
Explanation: The total number of empty spaces are 2*2=4 and the pieces to be set is 2 so there are 4C2 combinations ((4!/(2!*2!))=6) possible which is represented above.
Input: N = 1
Output: *
Approach: This problem can be solved by using recursion to generate all possible solutions. Now, follow the steps below to solve this problem:
- Create a function named allCombinations, which will generate all possible solutions.
- It will take an integer piecesPlaced denoting the number of total pieces placed, integer N denoting the number of pieces needed to be placed, two integers row and col denoting the row and column where the current piece is going to be placed and a string ans for storing the matrix where pieces are placed, as arguments.
- Now, the initial call to allCombinations will pass 0 as piecesPlaced, N, 0 and 0 as row and col and an empty string as ans.
- In each call, check for the base case, that is:
- If row becomes N and all pieces are placed, i.e. piecesPlaced=N. Then print the ans and return. Else if piecesPlaced is not N, then just return from this call.
- Now make two calls:
- One to add a ‘*’ at the current position, and one to leave that position and add ‘-‘.
- After this, the recursive calls will print all the possible solutions.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
void allCombinations(int piecesPlaced, int N, int row,
int col, string ans)
{
if (row == N) {
if (piecesPlaced == N) {
cout << ans;
}
return;
}
int nr = 0;
int nc = 0;
string x = "";
string y = "";
if (col == N - 1) {
nr = row + 1;
nc = 0;
x = ans + "*\n";
y = ans + "-\n";
}
else {
nr = row;
nc = col + 1;
x = ans + "*\t";
y = ans + "-\t";
}
allCombinations(piecesPlaced + 1, N, nr, nc, x);
allCombinations(piecesPlaced, N, nr, nc, y);
}
int main()
{
int N = 2;
allCombinations(0, N, 0, 0, "");
return 0;
}
|
Java
import java.io.*;
import java.util.*;
public class main {
public static void allCombinations(
int piecesPlaced,
int N, int row,
int col, String ans)
{
if (row == N) {
if (piecesPlaced == N) {
System.out.println(ans);
}
return;
}
int nr = 0;
int nc = 0;
String x = "";
String y = "";
if (col == N - 1) {
nr = row + 1;
nc = 0;
x = ans + "*\n";
y = ans + "-\n";
}
else {
nr = row;
nc = col + 1;
x = ans + "*\t";
y = ans + "-\t";
}
allCombinations(
piecesPlaced + 1, N,
nr, nc, x);
allCombinations(piecesPlaced, N,
nr, nc, y);
}
public static void main(String[] args)
throws Exception
{
int N = 2;
allCombinations(0, N, 0, 0, "");
}
}
|
Python3
def allCombinations(piecesPlaced, N, row, col, ans):
if row == N:
if piecesPlaced == N:
print(ans)
return;
nr = 0
nc = 0
x = ""
y = ""
if col == N - 1:
nr = row + 1
nc = 0
x = ans + "*\n"
y = ans + "-\n"
else:
nr = row
nc = col + 1
x = ans + "* "
y = ans + "- "
allCombinations(piecesPlaced + 1, N, nr, nc, x);
allCombinations(piecesPlaced, N, nr, nc, y);
N = 2
allCombinations(0, N, 0, 0, "")
|
C#
using System;
public class main {
public static void allCombinations(int piecesPlaced,
int N, int row,
int col, String ans)
{
if (row == N) {
if (piecesPlaced == N) {
Console.WriteLine(ans);
}
return;
}
int nr = 0;
int nc = 0;
String x = "";
String y = "";
if (col == N - 1) {
nr = row + 1;
nc = 0;
x = ans + "*\n";
y = ans + "-\n";
}
else {
nr = row;
nc = col + 1;
x = ans + "*\t";
y = ans + "-\t";
}
allCombinations(piecesPlaced + 1, N, nr, nc, x);
allCombinations(piecesPlaced, N, nr, nc, y);
}
public static void Main(string[] args)
{
int N = 2;
allCombinations(0, N, 0, 0, "");
}
}
|
Javascript
function allCombinations(piecesPlaced, N, row, col, ans) {
if (row == N) {
if (piecesPlaced == N) {
document.write(ans);
}
return;
}
let nr = 0;
let nc = 0;
let x = "";
let y = "";
if (col == N - 1) {
nr = row + 1;
nc = 0;
x = ans + "*<br>";
y = ans + "-<br>";
}
else {
nr = row;
nc = col + 1;
x = ans + "* ";
y = ans + "- ";
}
allCombinations(piecesPlaced + 1, N, nr, nc, x);
allCombinations(piecesPlaced, N, nr, nc, y);
}
let N = 2;
allCombinations(0, N, 0, 0, "");
|
Output: * *
- -
* -
* -
* -
- *
- *
* -
- *
- *
- -
* *
Time Complexity: O(2^M), where M=N*N
Auxiliary Space: 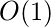
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...