Print a pair of numbers with the given Sum and Product
Last Updated :
20 Dec, 2022
Given a sum S and product P, the task is to print any pair of integers that has the sum S and the product P. If there exists no such pair, then print -1.
Examples:
Input: S = 5, P = 6
Output: 2, 3
Explanation:
Sum = 2 + 3 = 5, and
Product = 2 * 3 = 6
Input: S = 5, P = 9
Output: -1
Explanation:
No such pair exists
Approach: Let the pair be (x, y). Therefore, according to the problem, the given sum (S) will be (x + y) and the given product (P) will be (x * y)
If the pair is (x, y)
Given that product
P = x * y
y = P / x; (eq.. 1)
Given that sum
S = x + y
S = x + (P / x) from (eq..1)
x2 - Sx + P = 0
which is a quadratic equation in x.
Since this is a quadratic equation, we just need to find it’s roots, using the below equation.
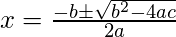
Here:
a = 1
b = -S
c = P
Therefore the above equation will be changed as:
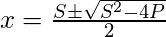
Below is the implementation of the above approach:
CPP
#include <bits/stdc++.h>
using namespace std;
void findRoots(int b, int c)
{
int a = 1;
int d = b * b - 4 * a * c;
double sqrt_val = sqrt(abs(d));
if (d > 0) {
double x = -b + sqrt_val;
double y = -b - sqrt_val;
int root1 = (x) / (2 * a);
int root2 = (y) / (2 * a);
if (root1 + root2 == -1 * b
&& root1 * root2 == c)
cout << root1 << ", " << root2;
else
cout << -1;
}
else if (d == 0) {
int root = -b / (2 * a);
if (root + root == -1 * b
&& root * root == c)
cout << root << ", " << root;
else
cout << -1;
}
else {
cout << -1;
}
cout << endl;
}
int main()
{
int S = 5, P = 6;
findRoots(-S, P);
S = 5, P = 9;
findRoots(-S, P);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void findRoots(int b, int c)
{
int a = 1;
int d = b * b - 4 * a * c;
double sqrt_val = Math.sqrt(Math.abs(d));
if (d > 0) {
double x = -b + sqrt_val;
double y = -b - sqrt_val;
int root1 = (int)(x) / (2 * a);
int root2 = (int) (y) / (2 * a);
if (root1 + root2 == -1 * b
&& root1 * root2 == c)
System.out.print( root1 + ", " + root2);
else
System.out.print( -1);
}
else if (d == 0) {
int root = -b / (2 * a);
if (root + root == -1 * b
&& root * root == c)
System.out.print(root+ ", "+root);
else
System.out.print(-1);
}
else {
System.out.print( -1);
}
System.out.println();
}
public static void main (String []args)
{
int S = 5, P = 6;
findRoots(-S, P);
S = 5;
P = 9;
findRoots(-S, P);
}
}
|
Python3
from math import sqrt
def findRoots(b, c):
a = 1
d = b * b - 4 * a * c
sqrt_val = sqrt(abs(d))
if (d > 0):
x = -b + sqrt_val
y = -b - sqrt_val
root1 = (x) // (2 * a)
root2 = (y) // (2 * a)
if (root1 + root2 == -1 * b
and root1 * root2 == c):
print(int(root1),",",int(root2))
else:
print(-1)
elif (d == 0):
root = -b // (2 * a)
if (root + root == -1 * b
and root * root == c):
print(root,",",root)
else:
print(-1)
else:
print(-1)
if __name__ == '__main__':
S = 5
P = 6
findRoots(-S, P)
S = 5
P = 9
findRoots(-S, P)
|
C#
using System;
public class GFG
{
static void findRoots(int b, int c)
{
int a = 1;
int d = b * b - 4 * a * c;
double sqrt_val = Math.Sqrt(Math.Abs(d));
if (d > 0) {
double x = -b + sqrt_val;
double y = -b - sqrt_val;
int root1 = (int)(x) / (2 * a);
int root2 = (int) (y) / (2 * a);
if (root1 + root2 == -1 * b
&& root1 * root2 == c)
Console.Write( root1 + ", " + root2);
else
Console.Write( -1);
}
else if (d == 0) {
int root = -b / (2 * a);
if (root + root == -1 * b
&& root * root == c)
Console.Write(root+ ", "+root);
else
Console.Write(-1);
}
else {
Console.Write( -1);
}
Console.WriteLine();
}
public static void Main (string []args)
{
int S = 5, P = 6;
findRoots(-S, P);
S = 5;
P = 9;
findRoots(-S, P);
}
}
|
Javascript
<script>
function findRoots(b, c)
{
var a = 1;
var d = b * b - 4 * a * c;
var sqrt_val = Math.sqrt(Math.abs(d));
if (d > 0)
{
var x = -b + sqrt_val;
var y = -b - sqrt_val;
var root1 = (x) / (2 * a);
var root2 = (y) / (2 * a);
if (root1 + root2 == -1 * b
&& root1 * root2 == c)
document.write(root1 + ", " + root2);
else
document.write(-1);
}
else if (d == 0)
{
var root = -b / (2 * a);
if (root + root == -1 * b
&& root * root == c)
document.write(root + ", " + root);
else
document.write(-1);
}
else
{
document.write(-1);
}
document.write("<br>");
}
var S = 5, P = 6;
findRoots(-S, P);
S = 5, P = 9;
findRoots(-S, P);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
As constant extra space is used.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...