Principal Component Analysis with Python
Last Updated :
22 Apr, 2023
Principal Component Analysis is basically a statistical procedure to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables.
Each of the principal components is chosen in such a way that it would describe most of them still available variance and all these principal components are orthogonal to each other. In all principal components, first principal component has a maximum variance.
Uses of PCA:
- It is used to find interrelations between variables in the data.
- It is used to interpret and visualize data.
- The number of variables is decreasing which makes further analysis simpler.
- It’s often used to visualize genetic distance and relatedness between populations.
These are basically performed on a square symmetric matrix. It can be a pure sums of squares and cross-products matrix Covariance matrix or Correlation matrix. A correlation matrix is used if the individual variance differs much.
Objectives of PCA:
- It is basically a non-dependent procedure in which it reduces attribute space from a large number of variables to a smaller number of factors.
- PCA is basically a dimension reduction process but there is no guarantee that the dimension is interpretable.
- The main task in this PCA is to select a subset of variables from a larger set, based on which original variables have the highest correlation with the principal amount.
- Identifying patterns: PCA can help identify patterns or relationships between variables that may not be apparent in the original data. By reducing the dimensionality of the data, PCA can reveal underlying structures that can be useful in understanding and interpreting the data.
- Feature extraction: PCA can be used to extract features from a set of variables that are more informative or relevant than the original variables. These features can then be used in modeling or other analysis tasks.
- Data compression: PCA can be used to compress large datasets by reducing the number of variables needed to represent the data, while retaining as much information as possible.
- Noise reduction: PCA can be used to reduce the noise in a dataset by identifying and removing the principal components that correspond to the noisy parts of the data.
- Visualization: PCA can be used to visualize high-dimensional data in a lower-dimensional space, making it easier to interpret and understand. By projecting the data onto the principal components, patterns and relationships between variables can be more easily visualized.
Principal Axis Method: PCA basically searches a linear combination of variables so that we can extract maximum variance from the variables. Once this process completes it removes it and searches for another linear combination that gives an explanation about the maximum proportion of remaining variance which basically leads to orthogonal factors. In this method, we analyze total variance.
Eigenvector: It is a non-zero vector that stays parallel after matrix multiplication. Let’s suppose x is an eigenvector of dimension r of matrix M with dimension r*r if Mx and x are parallel. Then we need to solve Mx=Ax where both x and A are unknown to get eigenvector and eigenvalues.
Under Eigen-Vectors, we can say that Principal components show both common and unique variance of the variable. Basically, it is variance focused approach seeking to reproduce total variance and correlation with all components. The principal components are basically the linear combinations of the original variables weighted by their contribution to explain the variance in a particular orthogonal dimension.
Eigen Values: It is basically known as characteristic roots. It basically measures the variance in all variables which is accounted for by that factor. The ratio of eigenvalues is the ratio of explanatory importance of the factors with respect to the variables. If the factor is low then it is contributing less to the explanation of variables. In simple words, it measures the amount of variance in the total given database accounted by the factor. We can calculate the factor’s eigenvalue as the sum of its squared factor loading for all the variables.
Now, Let’s understand Principal Component Analysis with Python.
To get the dataset used in the implementation, click here.
Step 1: Importing the libraries
Python
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
|
Step 2: Importing the data set
Import the dataset and distributing the dataset into X and y components for data analysis.
Python
dataset = pd.read_csv('wine.csv')
X = dataset.iloc[:, 0:13].values
y = dataset.iloc[:, 13].values
|
Step 3: Splitting the dataset into the Training set and Test set
Python
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
|
Step 4: Feature Scaling
Doing the pre-processing part on training and testing set such as fitting the Standard scale.
Python
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
|
Step 5: Applying PCA function
Applying the PCA function into the training and testing set for analysis.
Python
from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
explained_variance = pca.explained_variance_ratio_
|
Step 6: Fitting Logistic Regression To the training set
Python
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)
|
Output:

Step 7: Predicting the test set result
Python
y_pred = classifier.predict(X_test)
|
Step 8: Making the confusion matrix
Python
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
|
Step 9: Predicting the training set result
Python
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1,
stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1,
stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(),
X2.ravel()]).T).reshape(X1.shape), alpha = 0.75,
cmap = ListedColormap(('yellow', 'white', 'aquamarine')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
plt.title('Logistic Regression (Training set)')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legend()
plt.show()
|
Output:
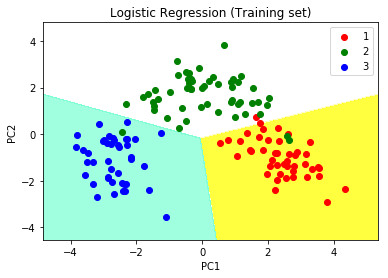
Step 10: Visualizing the Test set results
Python
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1,
stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1,
stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(),
X2.ravel()]).T).reshape(X1.shape), alpha = 0.75,
cmap = ListedColormap(('yellow', 'white', 'aquamarine')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
plt.title('Logistic Regression (Test set)')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legend()
plt.show()
|
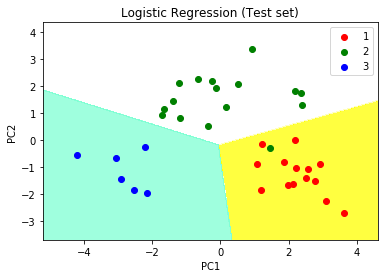
We can visualize the data in the new principal component space:
Python3
y = df.iloc[:, -1].values
colors = ["r", "g"]
labels = ["Class 1", "Class 2"]
for i, color, label in zip(np.unique(y), colors, labels):
plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], color=color, label=label)
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.legend()
plt.show()
7
|
This is a simple example of how to perform PCA using Python. The output of this code will be a scatter plot of the first two principal components and their explained variance ratio. By selecting the appropriate number of principal components, we can reduce the dimensionality of the dataset and improve our understanding of the data.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...