Prime Implicant chart for minimizing Cyclic Boolean functions
Last Updated :
10 Jun, 2021
Prerequisite – K-Map (Karnaugh Map), Implicants in K-Map
A functions is said to be a Cyclic Boolean Function if there is no Essential prime Implicant in its respective K-Map.
Properties of Cyclic functions:
- Every prime Implicant is of same size.
- Every minterm is covered by at least two prime Implicants (which means no essential prime Implicants).
- Having no essential prime Implicants means that there exist more than one minimized Solution / Expression for such functions, which will further be realized using digital circuits.
- For a cyclic function we can have two minimal forms with no overlapping of prime Implicants.
Example:
Find the minimal expression for the following function.
f(w, x, y, z) = 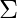 (0, 2, 4, 5, 10, 11, 13, 15)
(0, 2, 4, 5, 10, 11, 13, 15)

As we can see in the above K-Map that there exist no essential prime Implicants. Here we can use prime Implicant chart to solve it easily.
Steps to solve above function using prime Implicant chart:
- Step-1:
Draw prime Implicant chart as below.The horizontal entries denote the given minterms which are mapped against all prime Implicants (vertically).The square boxes are crossed (‘x’) whenever a prime Implicant covers a particular minterm in K-Map.
For example ‘WXZ’ prime Implicant is covering 13 and 15 therefore the corresponding squares are crossed(denoted by ‘x’).
Note that, A, B, C, D .., are variables used to denote all the prime Implicants.

- Step-2:
Arbitrarily choose any prime Implicant; check ( ) the prime Implicant and the corresponding covered minterms as well. Now delete the row of the prime Implicant and corresponding columns of its minterms.
) the prime Implicant and the corresponding covered minterms as well. Now delete the row of the prime Implicant and corresponding columns of its minterms.
In our example prime Implicant A is chosen which is covering minterms 2 and 10. Therefore. delete the row of A and the columns of 2 and 10. The arbitrarily chosen Prime Implicant (in our example A) must be present in the final minimal expression.


- Step-3:
Find all such prime Implicant which are being covered by other prime Implicant completely and remove their corresponding rows (since these are non essential prime Implicants.).
In our example H is covering {0, 4} and B is covering {0} it means H is covering all the minterms that are covered by B, so delete B. Similarly D is covering C completely, so delete C.


- Step-4:
Now follow the standard procedure of prime Implicant chart mentioned in the sub steps given below:
- Find the minterm which is covered by only one prime Implicant.
- Check (
 ) that minterm, its corresponding prime Implicant and all other minterms which are covered by that corresponding prime Implicant.
) that minterm, its corresponding prime Implicant and all other minterms which are covered by that corresponding prime Implicant.
- If all the minterms are checked (
 ) stop the procedure, otherwise goto sub-step-1.
) stop the procedure, otherwise goto sub-step-1.
Example-2: find the minimal expression for the following cyclic function.
f(x, y, z) = 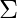 (0, 1, 2, 5, 6, 7)
(0, 1, 2, 5, 6, 7)

Step-1:
Draw prime Implicant chart.

Step-2:
A is chosen arbitrarily.Now the row of A and the columns of the corresponding minterms (0 and 2) are deleted.


Step-3:
Since B and F are completely covered by C and E respectively hence deleting prime Implicants B and F .

Step-4:
Now follow the standard procedure of prime Implicant chart mentioned in Example-1.
Minterm 1 is covered by prime Implicant C only therefore check ( ) C along with all the minterms which are covered by it (1 and 5).
) C along with all the minterms which are covered by it (1 and 5).
Minterm 6 is covered by prime Implicant E only therefore check ( ) E along with all the minterms which are covered by it (6 and 7).
) E along with all the minterms which are covered by it (6 and 7).

Now since all the min terms (1, 5, 6, 7) are checked( ) therefore stop the procedure.
) therefore stop the procedure.
Final Minimal Expression: A + C + E
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...