Probability in simple words is the prediction of the happening of an event before it has already happened. We do prediction in many things in our day-to-day life, like:
1) Predict the weather before going for a picnic.
2) Predict the outcome of the election.
3) Predict who is going to win the toss.
In all these situations we try to find the probability or chances of occurring of an event by considering all the conditions which are in favor of that event. From the above discussion probability can be defined mathematically as :
Probability is the branch of mathematics that tells us what are the chances for an event to occur. The probability of an event is a number between 0 and 1, where, 0 indicates the impossibility of the event and 1 indicates certainty. Therefore, 0 ≤ P(E) ≤ 1, where P(E) = Probability of an event to occur.
Some basic terminology used in probability are:
1. Experiment: An experiment is known as an event in which some well-defined outcome is expected. Also known as sample space. For example, sample space S is S = {H, T}, where H refers to head and T refers to Tail.
2. Trial: A trial is known as a single event that is performed to determine the outcome.
3. Outcome: Outcomes are the results of an experiment. For example, win/loss are possible outcomes of the cricket match.
4. Random experiment: A random experiment is an experiment whose outcome may not be predicted in advance. It may be repeated under numerous conditions.
5. Impossible Event: When the probability of an event is 0, then the event is known as an impossible event.
6. Sure Event: When the probability of an event is 1, then the event is known as a sure event.
Probability Formula
The experimental probability or empirical probability of an event is
Probability(E) = 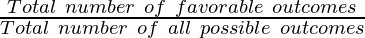
Alternatively,
P(E) = 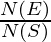
Here, P(E) = Probability of an event to occur
N(E) = Total number of favorable outcomes
N(S) = Total number of all possible outcomes
Now let’s move on to solving problems and understanding probability better.
Sample Problems
Question 1. Sumit is playing cricket with his friends, to decide who is going to bat is decided by tossing a coin, whichever wins the toss will bat first. Assuming Sumit and Mohit are captains of the two teams which have chosen heads and tails respectively. Find the chances of Sumit to bat first.
Solution:
We know, there are only two possible outcomes of the toss i.e. heads or tails.
Therefore, Sample space(s) = Total possible outcomes = {H, T}
Sumit needs heads to win the toss, therefore there is only one favorable outcome.
Probability of Sumit to win the toss = favorable outcome / total outcome
= 1/2 = 0.5
Question 2. Two dice are tossed. Find the probability that the total score is a prime number?
Solution:
Since, two dices are tossed therefore total no of combination = n(S) = (6 x 6) = 36 combinations.
Let us considered E be the event that the sum is a prime number.
All the favorable outcomes are (E) = {(1, 1), (1, 2), (1, 4), (1, 6), (2, 1),
(2, 3), (2, 5), (3, 2), (3, 4), (4, 1),
(4, 3), (5, 2), (5, 6), (6, 1), (6, 5)}
Therefore, n(E) = 15
Probability of score to be prime number = n(E)/n(S) = 15/36 = 5/12
Question 3. In a lottery box, there are 10 prizes and 25 blanks. A slip is drawn at random from the lottery box. What is the probability of getting a prize?
Solution:
Given: Total number of prize = 10
Total number of blanks = 25
So, the total number of possible outcomes(i.e., n(S)) are = 10 + 25 = 35
Total number of prizes, n(E) = 10
According to the formula
P(E) = n(E)/n(S) = 1035 = 27
Question 4. A bag contains 8 blue balls and some pink balls. If the probability of drawing a pink ball is half of the probability of drawing a blue ball then find the number of pink balls in the bag.
Solution:
Let us considered the number of pink balls be n.
The number of blue balls = 8.
Therefore, the total number of balls present in the bag = n + 8.
Now, the probability of drawing a pink ball, i.e. P(X) = n/n + 8
the probability of drawing blue ball, i.e. P(B) = 8/n + 8
According to the question, the probability of drawing pink
ball is half of the probability of drawing the blue ball
So, P(X) = P(B)/2
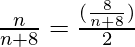
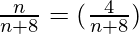
n = 4.
So, number of pink balls present in the bag is 4.
Question 5. Card numbered 1 to 20 are mixed up and then a card is drawn at random. What is the probability that the card drawn has a number which is a multiple of 3 or 5?
Solution:
Card are numbered from 1 to 20 therefore n(S) = {1, 2, 3, 4, …., 19, 20}.
Let us considered E be the event of getting a multiple of 3 or 5
So, n(E) = {3, 6, 9, 12, 15, 18, 5, 10, 20}.
According to the formula
P(E) = n(E)/n(S) = 9/20.
Question 6. One card is drawn from a deck of 52 cards, well-shuffled. Calculate the probability that the card will
(i) be an ace,
(ii) not be an ace.
Solution:
Well-shuffling ensures equally likely outcomes.
(i) There are 4 aces in a deck.
Let us considered E be the event the card drawn is ace.
The number of favorable outcomes to the event E = 4
The number of possible outcomes = 52
Therefore, P(E) = 4/52 = 1/13
(ii) Let us considered F be the event of ‘card is not an ace’
The number of favorable outcomes to F = 52 – 4 = 48
The number of possible outcomes = 52
Therefore, P(F) = 48/52 = 12/13
Question 7. In a simultaneous throw of a pair of dice. Find the probability of getting a total of more than 7.
Solution:
Total number of combinations for a pair of dice is = n(S) = (6 x 6) = 36
Let us considered E be the event of getting a total more than 7
= {(2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 3), (5, 4),
(5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
Therefore, P(E) = n(E)/n(S)
= 15/36 = 5/12.
Question 8. In a company of 364 workers, 91 are married. Find the probability of selecting a worker who is unmarried.
Solution:
Given,
Total workers (i.e. Sample space) = n(S) = 364
Total married workers = 91
Now, total workers who are unmarried = n(E) = 364 – 91 = 273
Method 1: So, the probability of unmarried worker P(NM) = n(E)/n(S) = 273/364 = 0.75
Method 2: P(M) + P(NM) = 1
Here, P(M) = 91/364 = 0.25
So, 0.25 + P(NM) = 1
P(NM) = 1 – 0.25 = 0.75
Question 9. From a bag of yellow and brown balls, the probability of picking a red ball is x/2. Find “x” if the probability of picking a brown ball is 2/3.
Solution:
Given, in the bag only yellow and brown balls.
P(picking a yellow ball) + P(picking a brown ball) = 1
x/2 + 2/3 = 1
3x + 4 = 6
3x = 2
Or, x = 2/3
Question 10. Two coins are tossed simultaneously for 360 times. The number of times ‘2 Tails’ appeared was three times ‘No Tail’ appeared and number of times ‘1 tail’ appeared is double the number of times ‘No Tail’ appeared. Find the probability of getting ‘Two tails’.
Solution:
Total number of outcomes = 360
Let us considered the number of times ‘No Tail’ appeared be z
Then, number of times ‘2 Tails’ appeared = 3z
Number of times ‘1 Tail’ appeared = 2z
Now, z + 2z + 3z = 360
6z = 360
z = 60
Hence, the probability of getting ‘two tails’ = (3 x 60)/360 = 1 /2
Share your thoughts in the comments
Please Login to comment...