Practice Problems on Potential Energy

In daily use, the potential word is used a lot for things or persons which show promise inside them. “Potential” shows the possibility for action. It gives an idea of stored energy that can be converted. This is the idea behind potential energy. This concept is an integral part of mechanics and allows us to theoretically measure the energy stored inside an object. Potential energy can come through any force. For example – a stretched or compressed spring has potential energy. An object sitting at some height possesses potential energy due to height. 

Potential Energy 

Potential energy is the energy possessed by an object due to its position or configuration. This energy is said to be stored inside the object. Usually, potential energy is released by an object by motion. For example, a stretched spring, when released, starts moving towards its natural position and starts acquiring speed. Due to this speed, it acquires kinetic energy. To further understand this, let’s consider a ball of mass “m”. 

This ball which was initially on the ground is taken to a height of “h”. External force in the form of gravity is acting on it. We know that work done by a force F on a displacement “s” on the object is given by, 

W = F.s

In this case, force is the force of gravity and displacement from the ground to the height “h”. 

F = mg, s = h 

Then, work done by gravity on the object is, 

W = -mgh

Potential energy is defined as the negative of this work. Denoting the potential energy V(h). 

V(h) = mgh

If the ball is dropped, in that case, the potential energy decreases, and the speed increases. This means the potential energy of the object is getting converted to kinetic energy. Let’s say the speed of the ball just before touching the ground is “v”. 

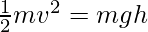
Potential Energy in a Spring

When the spring is kept normally, it is said to have 0 energy and is said to be in the equilibrium state. When it is stretched or compressed, and there is a certain displacement, say x, it will have certain potential energy saved in it which is given as,

P.E.= 1/2 (Kx²)

Where, K = Spring constant

x = displacement due to compression or expansion.

Let’s see some problems based on these concepts. 

Sample Problems

Question 1: A mass of 2Kg is taken from the ground to the height of 10m. Find the potential energy of the object.

Answer:

The potential energy of a mass ‘m’ at the height ‘h’ is given by, 

P = mgh 

Given: m = 2kg and g = 10 m/s² and h = 10m. 

Aim: Find the potential energy. 

Plugging in the values in the formula. 

P = mgh 

⇒ P = (2)(10)(10) 

⇒P = 200J

Thus, the potential energy of the object is 200J. 

Question 2: A mass of 5Kg is taken from the ground to the height of 100m. Find the potential energy of the object.

Answer:

The potential energy of a mass ‘m’ at the height ‘h’ is given by, 

P = mgh 

Given: m = 5kg and g = 10 m/s² and h = 100m. 

Aim: Find the potential energy. 

Plugging in the values in the formula. 

P = mgh 

⇒ P = (5)(10)(100) 

⇒P = 5000J

Thus, the potential energy of the object is 5000J. 

Question 3: A mass of 5Kg is taken from the ground for 5 m uphill on the wedge. The wedge makes an angle of 30° with the ground. Find the potential energy of the block. 

Answer:

The potential energy of a mass ‘m’ at the height ‘h’ is given by, 

P = mgh 

This wedge is in the form of a right-angled triangle. 

Figure 

Let’s say, h is the vertical height at which the box reaches, let the slanted length be L

L = 5 m 

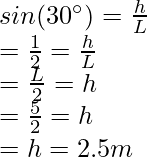
Given: m = 5kg and g = 10 m/s² and h = 2.5m. 

Aim: Find the potential energy. 

Plugging in the values in the formula. 

P = mgh 

⇒ P = (5)(10)(2.5) 

⇒P = 125J

Thus, the potential energy of the object is 125J.

Question 4: A mass of 10Kg is taken from the ground for 10m uphill on the wedge. The wedge makes an angle of 30° with the ground. Find the potential energy of the block. 

Answer:

The potential energy of a mass ‘m’ at the height ‘h’ is given by, 

P = mgh 

This wedge is in the form of a right-angled triangle. 

Figure 

Let’s say, h is the vertical height at which the box reaches, let the slanted length be L

L = 10m 

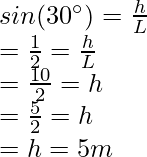
Given: m = 5kg and g = 10 m/s² and h = 5 m. 

Aim: Find the potential energy. 

Plugging in the values in the formula. 

P = mgh 

⇒ P = (5)(10)(5) 

⇒P = 250J

Thus, the potential energy of the object is 250J.

Question 5: Find the kinetic energy of the ball just before hitting the ground. Assume that initially, the ball was at a height of 10m, and its mass was 2Kg. 

Answer: 

Initially, at the height of 10m, the ball possesses potential energy. When it is dropped, it starts going towards the ground and its height starts decreasing. With decreasing height, velocity increases, and it acquires kinetic energy. 

Potential Energy at t = 0 

Potential energy will be given by, 

P = mgh

m = 2Kg, h = 10m and g = 10 m/s²

P = mgh 

⇒ P = (2)(10)(10) 

⇒P = 200J

When the ball is about to hit the ground, it’s potential energy has become zero and all the energy is converted into kinetic energy. 

Thus, K.E = 200J

Question 6: Find the velocity of the ball just before hitting the ground. Assume that initially, the ball was at a height of 100m, and its mass was 4Kg. 

Answer: 

Initially, at the height of 10m, the ball possesses potential energy. When it is dropped, it starts going towards the ground and its height starts decreasing. With decreasing height, velocity increases, and it acquires kinetic energy. 

Potential Energy at t = 0 

Potential energy will be given by, 

P = mgh

m = 4Kg, h = 100m and g = 10 m/s²

P = mgh 

⇒ P = (4)(100)(10) 

⇒P = 4000J

When the ball is about to hit the ground, its potential energy has become zero and all the energy is converted into kinetic energy. 

Thus, K.E = 4000J

The formula for K.E is, 

K.E =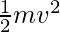 

m = 4Kg and v = ?. Plugging the values in the formula

K.E =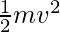 

⇒ 4000 =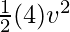 

⇒2000 = v²

⇒ v = 10√20 m/s

⇒ v = 20√5 m/s

Question 7: The entire potential energy of a ball is transformed into its kinetic energy by coming on the ground from a certain height. The height at which the ball was initially placed was 10m. The mass of the ball is 1 kg. Find the gain in the kinetic energy.

Solution:

Since, the all the potential energy present in the ball is transferred into its kinetic energy, 

Potential energy of the ball = Final gain in the kinetic energy

P= mgh

m= 1kg, h= 10m, g= 9.8m/sec²

P= 1× 10× 9.8 

P= 98 Joule

Therefore, the final gain in kinetic energy is 98 Joules.

K.E= 98 Joule.

Question 8: Explain the existence of potential energy,

a. Due to its position

b. Due to the state in which the object is.

Answer:

Potential energy can actually be present in two different cases,

a. Due to its position

Suppose an object is stable on the ground, now by applying some energy, it is taken at a certain height. The object present at a certain height will have energy saved in the form of potential energy. It is given as,

P.E= mgh

b. Due to the state in which object is present.

When a spring is kept in normal state, it is said to have 0 energy, but when the same spring is either compressed or stretched, it obtains potential energy which is given as,

P.E. = 1/2 (Kx²)

Where, x= displacement, K= Spring constant.

Question 9: A spring is stretched upto 9cm, the spring constant of the spring is 2 N/m. Find the value of Potential energy stored in the spring?

Solution:

The potential energy stored in a spring is given as,

P.E= 1/2 (Kx²)

K= 2 N/m, x= 9cm= 0.09m

P.E= 1/2 (2× (0.09)²)

P.E= 8.1 × 10^-3 Joules.

Question 10: Two objects are kept at different heights, first object is at 5meters and second object is placed at 15 meters. Which object has more Potential energy if the first object is 5 times heavier than the second?

Solution:

Object 1:

Height= 5 m, Mass= 5 m

P.E₁ = 5 m× 5× 9.8

P.E₁ = 245m Joules.

Object 2:

Height= 15 m, Mass= m

P.E₂ = 15× m× 9.8

P.E₂= 147m Joules.

Therefore, even when the first object is kept at lesser height, due to its weight, the first object has more potential energy.