Practice problems on finite automata | Set 2
Last Updated :
24 Apr, 2023
Que-1: Draw a deterministic and non-deterministic finite automate which either starts with 01 or end with 01 of a string containing 0, 1 in it, e.g., 01010100 but not 000111010. Explanation – Draw a DFA and NFA of same language whose strings only reach to the final state containing either 01 at start or at the end. If anything else is come then come out to the final state then it does not accept. NFA of the given string is as follows:  DFA of the given string is as follows:
DFA of the given string is as follows:  Here, q0 shows the initial state, q1, q2 are the transition states, and q3, q4, q5, q6, q7 are the transition and final states. Que-2: Draw a deterministic and non-deterministic finite automate which starts with 01 and ends with 01 of a string containing 0, 1 in it, e.g., 01000101 but not 000111001. Explanation – Draw a DFA and NFA of same language whose strings only reach to the final state containing 01 at start and at the end. If anything else is come then come out to the final state then it does not accept. NFA of the given string is as follows:
Here, q0 shows the initial state, q1, q2 are the transition states, and q3, q4, q5, q6, q7 are the transition and final states. Que-2: Draw a deterministic and non-deterministic finite automate which starts with 01 and ends with 01 of a string containing 0, 1 in it, e.g., 01000101 but not 000111001. Explanation – Draw a DFA and NFA of same language whose strings only reach to the final state containing 01 at start and at the end. If anything else is come then come out to the final state then it does not accept. NFA of the given string is as follows:  DFA of the given string is as follows:
DFA of the given string is as follows:
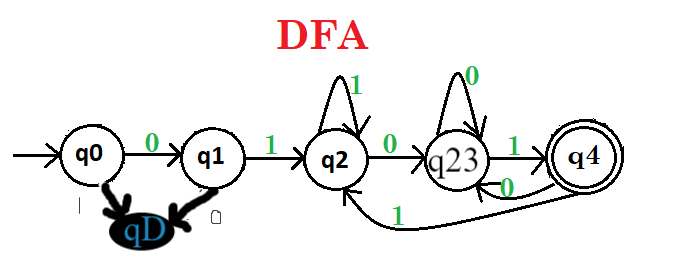
Here, q0 shows the initial state, q1, q2, q3 are the transition states, and q4, q5 are the transition and final states. Que-3: Draw a deterministic finite automata which recognize a string containing binary representation 0, 1 in the form of multiple 2, e.g., 1010 but not 01101. Explanation – Draw a DFA whose strings only reach to the final state containing 0 at the end that means number is multiple of 2. If anything else is come then come out to the final state then it does not accept. DFA of the given string is as follows:  Here, q0 shows the initial and final state, q1 is the transition states. Que-4: Draw a deterministic finite automata which recognize a string containing binary representation 0, 1 in the form of multiple 3, e.g., 1001 but not 1000. Explanation – Draw a DFA whose string only reach to the final state containing binary number is multiple of 3. If anything else is come then come out to the final state then it does not accept. DFA of the given string is as follows:
Here, q0 shows the initial and final state, q1 is the transition states. Que-4: Draw a deterministic finite automata which recognize a string containing binary representation 0, 1 in the form of multiple 3, e.g., 1001 but not 1000. Explanation – Draw a DFA whose string only reach to the final state containing binary number is multiple of 3. If anything else is come then come out to the final state then it does not accept. DFA of the given string is as follows:  Here, q0 shows the initial and final state, q1, q2 are the transition states. Read – Practice problems on finite automata
Here, q0 shows the initial and final state, q1, q2 are the transition states. Read – Practice problems on finite automata
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...