Powers of two and subsequences
Last Updated :
19 Sep, 2023
Given an array of size N, find count of subsequences which when multiplied result in a number which is a power of 2. Examples:
Input : A[] = {1, 2, 3}
Output : 3
Explanation: There are 3 such subsequences {1},
{2} and {1, 2}.
Input : A[] = {3, 5, 9}
Output : 0
Explanation: There is no such subsequence.
From the properties of power of two, we can see that it can be expressed only as a product of numbers which itself is power of 2. So first we traverse the array and count the total of numbers in the array which are power of two. Let’s say there are N such numbers in the array. We can either choose 1 or 2 or 3 or … or N such numbers to get a subsequence which is when multiplied results in a number which is power of two.
Therefore the required answer will be:
answer = 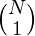 +
+ 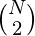 + … +
+ … + 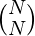 answer=
answer= 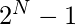
Below is the implementation of above idea.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPowerOf2(int num)
{
if (num == 0)
return false;
if (num == 1)
return true;
if (num & (num - 1))
return false;
return true;
}
int countSubsequence(int a[], int size)
{
int count = 0;
for (int i = 0; i < size; i++)
if (isPowerOf2(a[i]))
count++;
return (int)(pow(2, count)) - 1;
}
int main()
{
int a[] = { 1, 2, 3 };
cout << countSubsequence(a, 3) << endl;
int b[] = { 3, 5, 9 };
cout << countSubsequence(b, 3) << endl;
return 0;
}
|
Java
import java.io.*;
import java.math.*;
class GFG {
static boolean isPowerOf2(int num)
{
if (num == 0)
return false;
if (num == 1)
return true;
if (num / 2 == (num - 1) / 2)
return false;
return true;
}
static int countSubsequence(int a[],
int size)
{
int count = 0;
for (int i = 0; i < size; i++)
if (isPowerOf2(a[i]))
count++;
return (int)(Math.pow(2, count)) - 1;
}
public static void main(String args[])
{
int a[] = { 1, 2, 3 };
System.out.println(countSubsequence(a, 3));
int b[] = { 3, 5, 9 };
System.out.println(countSubsequence(b, 3)) ;
}
}
|
Python
def isPowerOf2(num) :
if (num == 0) :
return False
if (num == 1) :
return True
if (num & (num - 1)) :
return False
return True
def countSubsequence(a, size) :
count = 0
for i in range(0,size) :
if (isPowerOf2(a[i])) :
count = count + 1
return (int)(pow(2, count)) - 1
a = [ 1, 2, 3 ];
print countSubsequence(a, 3)
b = [ 3, 5, 9 ]
print countSubsequence(b, 3)
|
C#
using System;
class GFG {
static bool isPowerOf2(int num)
{
if (num == 0)
return false;
if (num == 1)
return true;
if (num / 2 == (num - 1) / 2)
return false;
return true;
}
static int countSubsequence(int []a,
int size)
{
int count = 0;
for (int i = 0; i < size; i++)
if (isPowerOf2(a[i]))
count++;
return (int)(Math.Pow(2, count)) - 1;
}
public static void Main()
{
int []a = { 1, 2, 3 };
Console.WriteLine(countSubsequence(a, 3));
int []b = { 3, 5, 9 };
Console.WriteLine(countSubsequence(b, 3)) ;
}
}
|
PHP
<?php
function isPowerOf2( $num)
{
if ($num == 0)
return false;
if ($num == 1)
return true;
if ($num & ($num - 1))
return false;
return true;
}
function countSubsequence( $a, $size)
{
$count = 0;
for($i = 0; $i < $size; $i++)
if (isPowerOf2($a[$i]))
$count++;
return pow(2, $count) - 1;
}
$a = array(1, 2, 3);
echo countSubsequence($a, 3) ,"\n";
$b = array(3, 5, 9);
echo countSubsequence($b, 3) ;
?>
|
Javascript
<script>
function isPowerOf2(num)
{
if (num == 0)
return false;
if (num == 1)
return true;
if (parseInt(num / 2, 10) == parseInt((num - 1) / 2, 10))
return false;
return true;
}
function countSubsequence(a, size)
{
let count = 0;
for (let i = 0; i < size; i++)
if (isPowerOf2(a[i]))
count++;
return (Math.pow(2, count)) - 1;
}
let a = [ 1, 2, 3 ];
document.write(countSubsequence(a, 3) + "</br>");
let b = [ 3, 5, 9 ];
document.write(countSubsequence(b, 3)) ;
</script>
|
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...