When an external force works to accomplish work, such as moving a body from one location to another against a force such as spring force or gravitational force, that work is collected and stored as the body’s potential energy. When the external force is removed, the body moves, acquiring kinetic energy and losing a corresponding amount of potential energy. As a result, the total kinetic and potential energy is preserved. Conservative forces are forces of this type. Spring force and gravitational force are two examples of these forces.
The Coulomb force is a conservative force that exists between two (stationary) charges. Both have an inverse-square relationship with respect to distance, with the only difference being the proportionality constants. The masses in the formulation of gravitational law are substituted by charges in the expression of Coulomb’s law. Thus, the electrostatic potential energy of a charge in an electrostatic field is defined in the same way as the gravitational potential energy of a mass in a gravitational field is.
What is an Electrostatic Potential?
The work done by an external force to carry a unit positive charge from infinity to a location is equal to the electrostatic potential (V) at that point is called the Electrostatic Potential.
Electric potential energy is a scalar quantity with no direction and only magnitude.
It is symbolized by V and has the dimensional formula [ML2T-3A-1].
Electric Potential Due to a Point Charge
Consider the origin of a point charge Q. Take Q to be positive. With position vector r from the origin, we want to find the potential at any point P. To do so, we must compute the amount of work required to transport a unit positive test charge from infinity to point P. When Q > 0, the work done on the test charge against the repulsive force is positive. We choose a handy path – along the radial direction from infinity to point P – since the work is done is independent of the path.

Work done in bringing a unit positive test charge from infinity to the point P, against the repulsive force of charge Q (Q > 0), is the potential at P due to the charge Q.
The electrostatic force on a unit positive charge at some intermediate point P′ on the path equals to
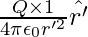
where 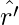 is the unit vector along OP′ therefore, work done against this force from r′ to r′ + ∆r′ can be written as
is the unit vector along OP′ therefore, work done against this force from r′ to r′ + ∆r′ can be written as
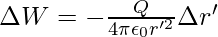
The negative sign represents ∆r′ < 0, ∆W is positive . Total work done (W) by the external force is determined by integrating the above equation both side, from r′ = ∞ to r′ = r,
![Rendered by QuickLaTeX.com W=-\int_{∞}^{r} \frac{Q}{4\pi\epsilon_0r'^2}d{r'}\\ W=\left[\frac{Q}{4\pi\epsilon_0r'}\right]_∞^r\\ W=\frac{Q}{4\pi\epsilon_0r}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d2e0180c3df582bd6cbe1919ff24155a_l3.png)
The potential at P due to the charge Q can be expressed as
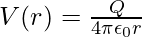
Potential Energy of a System of Charges
Consider the simple situation of two charges, q1 and q2, with position vectors r1 and r2 relative to a point. Let’s calculate the work that went into putting this arrangement together (from the outside). This means that first start with the charges q1 and q2 at infinity and then figure out how much work done by an external agency to get the charges to the provided destinations. Assume that the charge q1 is first transferred from infinity to r1. Because there is no external field against which work must be performed, the amount of work required to bring q1 from infinity to r1 is zero. This charge produces a potential in space that can be written as,
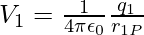

3 Potential energy of a system of charges q1 and q2 is directly proportional to the product charges and inversely to the distance between them.
where r1P is the distance of a point P in space from the location of q1. From the definition of potential, work done in bringing charge q2 from infinity to the point r2 is q2 times the potential at r2 due to q1,
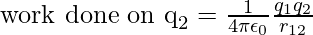
where r12 is the distance between points 1 and 2. Since electrostatic force is conservative, this work gets collected in the form of the potential energy of the system. Thus, the potential energy of a system of two charges q1 and q2 can be written as,
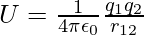 ……..(1)
……..(1)
Clearly, the potential energy U would be the same if q2 was transferred first to its current location and q1 was brought later.
Potential energy is positive if q1 q2 > 0. This is to be expected, because the electrostatic force is repulsive for like charges (q1 q2 > 0), and a positive amount of effort must be done against it to get the charges from infinity to a finite distance apart. The electrostatic force is attractive for dissimilar charges (q1q2< 0). To take the charges from the specified point to infinity, a positive quantity of work against this force is required. In other words, the reverse path (from infinity to the present places) requires a negative amount of work, hence the potential energy is negative.

The potential energy of a system of three charges.
Equation (1) can be easily generalized to any number of point charges in a system. Calculate the potential energy of a system with three charges q1, q2, and q3 at distances r1, r2, and r3 respectively. There is no work required to bring q1 first from infinite to r1. Bring next, bring q2 to r2 from infinity. As previously stated, the work completed in this step is
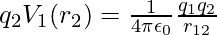 ……(2)
……(2)
The charges q1 and q2 generate a potential, which at any point P can be written as
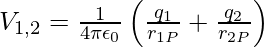
Work done next in bringing q3 from infinity to the point r3 is q3 times V1,2 at r3 can be written as,
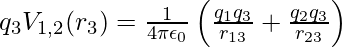 …….(3)
…….(3)
The total work done in collecting the charges at the given locations is obtained by adding equations (2) and (3),
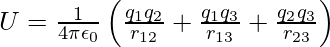
The final formula for U is independent of the method in which the configuration is formed due to the conservative nature of the electrostatic force (or, equivalently, the path independence of work done). The potential energy is a property of the current state of configuration, not the method by which it was produced.
Potential due to a System of Charges

Potential at a point due to a system of charges is the sum of potentials due to individual charges.
Suppose a system of charges q1, q2,…, qn with position vectors r1, r2,…, rn relative to some origin. The potential V1 at P due to the charge q1 is
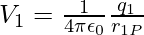
where r1P is the distance between q1 and P.
Similarly, the potential V2 at P due to q2 and V3 due to q3 can be written as,
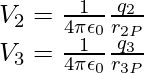
where r2P and r3P are the distances of P from charges q2 and q3 , respectively; and so on for the potential due to other charges. By the superposition principle, the potential V at P due to the total charge configuration is the algebraic sum of the potentials due to the individual charge that is,
V = V1 + V2 + V3 +…… + Vn
The above expression can be expressed as,
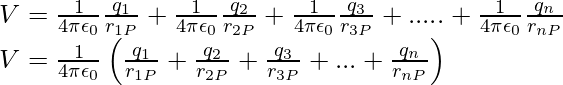
A continuous charge distribution with a charge density ρ (r), must be divided into small volume elements of size ∆v, each carrying a charge ρ ∆v. Then calculate the potential due to each volume element and add (or, more precisely, integrate) all of these contributions to get the total potential due to the distribution.
Sample Problems
Problem 1: Two charges 3 × 10–8 C and –2 × 10–8 C are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Solution:
Let us take the origin O at the location of the positive charge. The line joining the two charges is taken to be the x-axis; the negative charge is taken to be on the right side of the origin.

Let P be the expected point on the x-axis where the potential is zero. If x is the x-coordinate of P, and therefore x must be positive. If x lies between O and A, then
![Rendered by QuickLaTeX.com \frac{1}{4\pi\epsilon_0}\left[\frac{3\times10^{-8}}{x\times10^{-2}}-\frac{2\times10^{-8}}{(15-x)\times10^{-2}}\right]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f3d6efb38825d094e0ce8c0299faaff3_l3.png)
Rearrange the above equation to find the value of x,
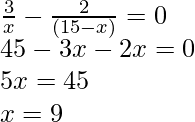
which gives x = 9 cm.
If x lies on the extended line OA, the required condition is
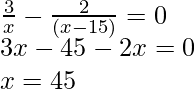
which results x = 45 cm.
On the side of the negative charge, an electric potential is zero at 9 cm and 45 cm away from the positive charge.
Problem 2: Figures (a) and (b) show the field lines of a positive and negative point charge respectively.

(a) Give the signs of the potential difference VP – VQ; VB – VA.
(b) Give the sign of the potential energy difference of a small negative charge between the points Q and P; A and B.
(c) Give the sign of the work done by the field in moving a small positive charge from Q to P.
(d) Give the sign of the work done by the external agency in moving a small negative charge from B to A.
(e) Does the kinetic energy of a small negative charge increase or decrease in going from B to A?
Solution:
(a) As V ∝ (1/r) and VP> VQ. Thus, (VP – VQ) is positive. Also, VB is less negative than VA. Thus, VB > VA or (VB – VA) is positive.
(b) A tiny negative charge will be attracted towards a positive charge. The negative charge moves from higher potential energy to lower potential energy. Therefore, the sign of potential energy difference of a small negative charge between Q and P is positive. Similarly, VA > VB and hence the sign of potential energy differences are positive.
(c) In moving a small positive charge from Q to P, work has to be done by an external agency against the electric field. Therefore, work done by the field is negative.
(d) In moving a small negative charge from B to A work has to be done by the external agency. It is positive.
(e) Due to the force of repulsion on the negative charge, velocity decreases and hence the kinetic energy decreases in going from B to A.
Problem 3: A 500 µC charge is at the center of a square of side 10 cm. Find the work done in moving a charge of 10 µC between two diagonally opposite points on the square.
Solution:
Because these two locations are at equipotential, the work done in transporting a charge of 10 C between two diagonally opposite spots on the square will be zero.
Problem 4: (a) Can two equipotential surfaces intersect each other? Give reasons.
(b) Two charges -q and + q are located at points A (0, 0, – a) and B (0, 0, +a) respectively. How much work is done in moving a test charge from point P (7, 0, 0) to Q (-3,0,0)?
Solution:
(a) No, if they intersect, the electric field will be in two distinct directions, which is incorrect. If they cross, there will be two potential values at the same point of intersection. Because this isn’t conceivable, two equipotential surfaces can’t meet.
(b) Work done will be zero since both points P and Q are on the dipole’s equatorial line, which has V = 0 at all points. Furthermore, because any charge’s force is perpendicular to the equatorial line, no work is done.
Problem 5: “For any charge configuration, equipotential surface through a point is normal to the electric field.” Justify.
Solution:
Work done in moving a charge over an equipotential surface is zero, hence a point on it will be normal to the electric field.
W = Fs cos θ
∴ cos θ = 0
or
θ = 90o
Problem 6: Why must the electrostatic potential inside a hollow charged conductor be the same at every point?
Solution:
Because the electric field inside the hollow charged conductor is zero, no work is done in moving a small test charge within the conductor. As a result, the electrostatic potential inside a hollow charged conductor remains constant.
Share your thoughts in the comments
Please Login to comment...