A vector is a quantity that has both magnitude and direction. Vectors allow us to describe the quantities which have both direction and magnitude. For example, velocity and position. These quantities are useful in describing the motion and the position of a particle that is moving in a plane. All the vectors follow the laws of parallelogram addition and triangle law. These laws allow us to perform arithmetic on the vectors. The position and the change in position (denoted by displacement) are the entities that use these concepts to describe the motion of a particle. Let’s understand them in detail.
Scalars and Vectors
In physics, quantities are classified in terms of vectors and scalars. The difference between them is that the quantities which have directions along with their magnitude associated with them are called vectors. A scalar quantity is just magnitude. In the case of scalar quantities, the arithmetic operations like addition, subtraction, or multiplication are performed in the same way as done with real numbers. For example, the sum of two scalar quantities with values 0.1 and 0.3 is given as 0.4. These rules do not apply to vector quantities. Their addition and subtraction are not as simple as scalar quantities.
The table given below shows some examples of scalar and vector quantities.
| Scalar Quantities | Vector Quantities |
| Length | Velocity |
| Speed | Force |
| Mass | Weight |
| Density | Pressure |
| Energy | Acceleration |
Laws of Addition and Subtraction of Vectors
Two vectors cannot be added by the usual arithmetic procedures, since the vectors contain directions. These vectors can be added using the laws of vector addition. For two vectors P and Q, their addition is given by vector R,
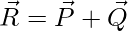
If the angle between the two vectors is θ, then the magnitude of the resultant vector is given by,
R2 = |P|2 + |Q|2 + 2|P||Q|cos(θ)
The angle that the resultant vector makes with the vector P, is given by,
Θ = tan-1(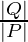

Vector Multiplication by a constant
Multiplication of a vector with a constant does not change its direction. Instead, this kind of multiplication serves to scale the vector. If the constant multiplied by the vector is greater than 1, the vector increases in its length, while it decreases in length when the constant is less than 1.
Motion in a Plane
When an object moves in a plane, it changes its position, and it is essential to define quantities that can be used to describe where the object is in the plane. The motion also requires direction. For example, suppose an object is moving as shown in the figure below. Now, to describe the position of the object, two things are required — direction and distance from the origin. Simply saying that the object is at a distance of 5 m from the origin is not enough.

This object will be described as 5 m in the North-East direction. Thus, to denote the position of an object, a vector is required. This vector is called a position vector. The diagram below shows the trajectory of an object moving in the plane. Let P and P’ be the positions of the object at time “t” and “t’“. The figure given below shows the position P and P’ with respect to the origin.

When the points P and P’ are joined by a straight line with origin O. The line segments OP and OP’ denote the position vectors. Vector OP is denoted by r and OP’ is denoted by r’. If the object moves from P to P’ in time “t”. Then, the displacement is given by the change in position vector. The vector denoting the change in position vector is also called the displacement vector.

Note: The Displacement vector only depends upon the initial and final position vectors. If an object travels a path and comes back to the same initial position, in that case the displacement is considered to be zero. The figure above shows an object traveling along a large path and coming back to the same point. In this case, the displacement is zero.
The magnitude of the displacement vector is less than or equal to the distance traveled by the particle between its initial and final positions.

Assume that a particle travels from point A to point B along the path traveled as shown in the above figure. In this case, displacement is given by the line joining the two points. Thus, it can be said that the displacement between two points is the shortest distance between those points.
Sample Problems
Question 1: Let’s say A = 4i + 3j and B = 5i + 4j. Find the resultant vector from the addition of these two vectors.
Answer:
Given:
A = 4i + 3j
B = 5i + 4j.
The resultant of these two vectors is given by,
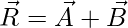
Plugging the vectors into this equation,
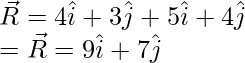
Question 2: Let’s say A = 5i + 5j and B = 3i + 3j. Find the resultant vector from the addition of these two vectors.
Answer:
Given:
A = 5i + 5j
B = 3i + 3j.
The resultant of these two vectors is given by,
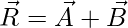
Plugging the vectors into this equation,
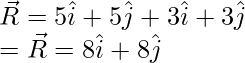
Question 3: Let’s say there are two vectors A and B, where |A| = 3 and |B| = 4 and the angle between them is given by 60°. Find the magnitude and direction of the resultant vector.
Answer:
Given:
|A| = 3
|B| = 4.
θ = 60°
The resultant of these two vectors is given by,
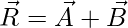
R2 = |A|2 + |B|2 + 2|A||B|cos(θ)
The angle is given by, θ = tan-1(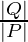
Plugging the vectors into these equations,
R2 = |A|2 + |B|2 + 2|A||B|cos(θ)
⇒ R2 = 32 + 42 + 2(3)(4)cos(60)
⇒ R2 = 25 + 12
⇒ R2 = 37
⇒ R = √37
θ = tan-1(
⇒ θ = tan-1(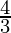
⇒ θ = 53°
Question 4: Let’s say there are two vectors A and B, where |A| = 24 and |B| = 10 and the angle between them is given by 90°. Find the magnitude and direction of the resultant vector.
Answer:
Given:
|A| = 24
|B| = 10.
θ = 90°
The resultant of these two vectors is given by,
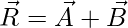
R2 = |A|2 + |B|2 + 2|A||B|cos(θ)
The angle is given by, θ = tan-1(
Plugging the vectors into these equations,
R2 = |A|2 + |B|2 + 2|A||B|cos(θ)
⇒ R2 = 242+ 102 + 2(24)(10)cos(90)
⇒ R2 = 576 + 100
⇒ R2 = 676
⇒ R = 26
θ = tan-1(
⇒ θ = tan-1(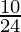
Question 5: The position vector of the particle moving in a plane is given by,
r = t2i + 3tj
Find the displacement between t =1 and t = 4 seconds.
Answer:
Displacement only depends on the initial and final position of the particle.
Given:
r = t2i + 3tj
at t = 1
ri = i + 3j
At t = 4
rf = 16i + 12j
Displacement between these position will be given by the difference of their position vectors.
r = rf – ri
⇒r = 16i + 12j -(i + 3j)
⇒ r = 15i + 9j
Question 6: The position vector of the particle moving in a plane is given by,
r = t2i + 3tj
Find the displacement between t =1 and t = 4 seconds.
Answer:
Displacement only depends on the initial and final position of the particle.
Given:
r = t2i + 3tj
at t = 1
ri = i + 3j
At t = 4
rf = 16i + 12j
Displacement between these position will be given by the difference of their position vectors.
r = rf – ri
⇒r = 16i + 12j -(i + 3j)
⇒ r = 15i + 9j
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...