Polytime Manyone reduction: Clique to E-TM
Last Updated :
30 Jun, 2020
Prerequisite –
Clique is NP
A Polynomial-time reduction is a method for solving one problem using another.
E-TM = {<M> : M is a TM and
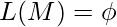
}
CLIQUE = {<G, k> : graph G has a clique with at least k vertices}.
Note –
Since CLIQUE is NP => some NDTM
CLIQUE accepts CLIQUE.
Reduction(<G, k>)
construct the following machine M
M(x):
1. Run NDTMCLIQUE on input <G, k>.
2. If NDTMCLIQUE accepts; M rejects x.
3. Else; M accepts x.
return <M>
We convert the instance <G, k>
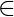
CLIQUE to a TM <M>
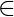
E-TM. And <G, k>
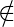
CLIQUE to a TM <M>
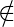
E-TM.
Correctness:
i. <G, k> 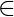 CLIQUE => M rejects all input x => L(M)=
CLIQUE => M rejects all input x => L(M)= 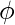 => <M>
=> <M> 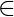 E-TM.
ii. <G, k>
E-TM.
ii. <G, k> 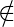 CLIQUE => M accepts all input x => L(M)
CLIQUE => M accepts all input x => L(M)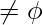 => <M>
=> <M> 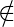 E-TM.
E-TM.
Hence, reduction is correct.
Polytime –
The reduction involves describing the construction of a new
Turing machine M for input <G, k>. We don’t run the machine on the input. Hence, the reduction is polytime.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...