Poisson’s Ratio is the negative ratio of transversal strain or lateral strain to the longitudinal strain of a material under stress. When a material particularly a rubber-like material undergoes stress the deformation is not limited to only one direction, rather it happens along both transversal and longitudinal directions. In this situation, material scientists are curious to know the ratio of transversal and longitudinal deformation that occurred in the object to know about the strength of the material.
In this article, we will learn about the longitudinal and transversal strain, the calculation of the Poisson Ratio, and other related aspects in detail.
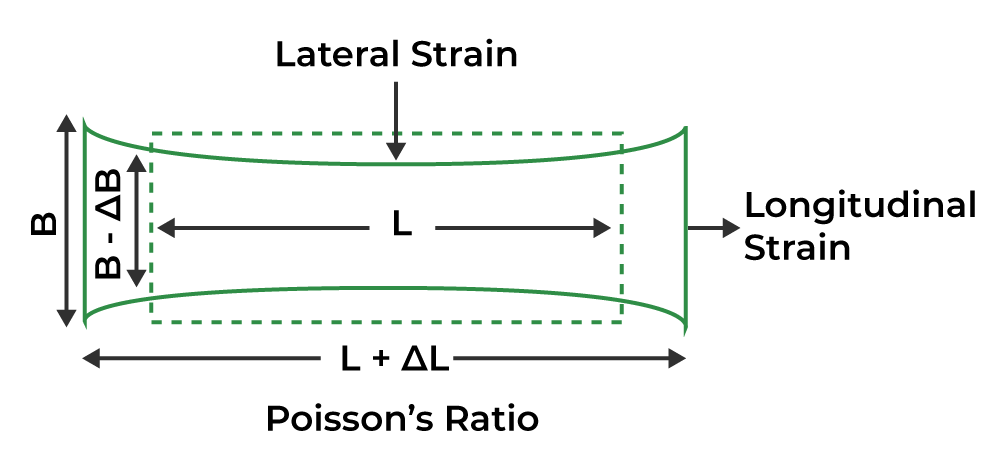
What is Poisson’s Ratio
Poisson’s ratio is the ratio of the amount of transversal expansion to the amount of axial compression for small values of these changes.
Poisson Ratio Definition
Poisson Ratio is defined as the negative ratio of the transversal strain to the longitudinal strain. It basically compares the change in the breadth of an object with respect to the change in the length of the object. It gives an idea about the strength of a material.
Longitudinal and Transversal Strain
When Stress is applied the change in dimension is seen along the direction of the stress applied and also the direction perpendicular to the stress applied. Let’s say when we apply tension stress on a horizontal bar, the length of the bar will increase along the direction of the applied stress. This is called Longitudinal Strain. Along with the increase in length, you will observe that the bar becomes thin in between i.e. the breadth of the bar decreases. This is what we call Transversal Strain. Both longitudinal and transversal strain go hand in hand but not at the same rate. To measure the relativeness of longitudinal and transversal strain we use Poisson’s Ratio.
Longitudinal Strain is given by εl = ΔL / L and it is positive as there is an increase in length.
Transversal Strain is given by εt = ΔB / B and it is negative as breadth decreases on applying tensile stress.
Now in the below sections, we will learn about Poisson Ratio in detail.
As stated in its definition, Poisson Ratio is given as the negative of the ratio of the transversal strain to the longitudinal strain its formula is mentioned below:
ν = -εt/εl
Where,
- ν is Poisson’s Ratio
- εt is Transversal Strain, and
- εl is Longitudinal Strain.
The negative sign in the ratio is used to make the ratio positive because the numerator i.e. transversal strain is generally negative due to a decrease in breadth. Thus Poisson’s Ratio is generally positive in nature, however in the case of material whose thickness increases on applying tensile stress such as polymers then that material will have a negative Poisson Ratio. Poisson Ratio is an scalar quantity.
Unit of Poisson Ratio: Since the Poisson Ratio is a ratio change in the length along transversal and longitudinal directions it has no unit.
Dimension of Poisson Ratio: Since there is no unit of Poisson Ration, there is no dimension of Poisson Ratio.
Poisson Effect
The Poisson effect is a phenomenon in which a material expands in directions perpendicular to the direction of compression. Poisson’s ratio is a measure of this phenomenon. When a material is stretched rather than crushed, it tends to contract in directions that are transverse to the stretching direction.
Poisson’s Ratio Values for Different Materials
Poisson’s Ratio is a scalar and a unitless quantity. It has a positive magnitude for tensile deformation while it has a negative value for auxetic materials like polymer.
The minus sign in Poisson’s Ratio formula indicates that the ratio of the transversal strain to the longitudinal strain is always positive.
Poisson’s Ratio Range
The range of Poisson’s Ratio value lies between -1.0 to +0.5. However, the value of Poisson’s ratio for most materials is between 0 and 0.5.
For plastics, the Poisson’s Ratio is in the range of 0 to 0.5. When the Poisson’s Ratio is 0, there is no reduction in diameter or, to put it another way, no lateral contraction occurs when the material is elongated, but the density decreases.
When the diameter of the material drops during the elongation process or when the material is elastomeric, a value of 0.5 implies that the volume of the material or item will remain the same or constant.
The following table shows the various Poisson’s Ratios for various materials.
|
Material
|
Poisson’s Ratio
|
|
Rubber
|
0.49
|
|
Gold
|
0.43
|
|
Clay
|
0.37
|
|
Copper
|
0.33
|
|
Aluminum
|
0.32
|
|
Cast Iron
|
0.24
|
|
Concrete
|
0.2
|
|
Cork
|
0
|
Poisson’s Ratio is usually positive since most common materials get narrower in the opposite or cross direction when stretched. Most materials resist changes in volume, as defined by the bulk modulus K or also known as B, more than changes in shape, as determined by the shear modulus G. The shape distortion also causes the interatomic connections to realign.
Applications of Poisson’s Ratio
Poisson’s Ratio is majorly used to analyze the strength of the material. However, it has got some other applications also which are mentioned below:
1. Poission’s Ratio in Bending
While bending a bar, the curvature of the bar perpendicular to the bending is governed by Poisson’s Ratio, while in the case of rubber anticlastic curvature i.e. convex along the longitudinal plane and concave along the perpendicular plane is observed.
2. Poisson’s Ratio in Anisotropic Material
Anisotropic Material is those which have direction-dependent properties. Examples include crystals, honeycombs, etc. In such objects, the Poisson’s Ratio is also direction dependent. Also, it can take any arbitrary large positive or negative value under the defined positive strain energy density.
3. Poisson’s Ratio in Viscoelastic Material
The viscoelastic material goes under creep which is a time-dependent phenomenon. In this case, Poisson’s Ratio is a function of time and also the frequency and the phase angle if there is sinusoidal deformation in the viscoelastic material.
4. Poisson’s Ratio in Phase Transformation
The Poisson’s Ratio of material is significantly affected by its phase transformation. At the point of phase transformation, the value of Poisson’s Ratio starts decreasing significantly and can even take a negative value as the bulk modulus of a material reduces at Phase Transformation Point.
People Also View:
Poisson’s Ratio – Solved Examples
Problem 1: The longitudinal strain for a wire is 0.02 and its Poisson ratio is 0.6. Find the lateral strain in the wire.
Solution:
Given:
Longitudinal strain of wire = 0.02
Poisson ratio = 0.6
The Poisson’s Ratio formula is as follows:
ν = lateral strain/longitudinal strain
Substitute the given values to find the lateral strain.
0.6 = Lateral strain / 0.02
Lateral strain = 0.012
Hence, the lateral strain in the wire is 0.012.
Problem 2: What is the maximum and minimum values of Poisson’s ratio for a metal?
Solution:
The Poisson’s Ratio formula is as follows:
ν = Lateral strain/longitudinal strain
It is always positive because if we apply force in longitudinal strain, lateral strain always decreases for metals. It lies between 0 to 0.5.
Problem 3: Is Poisson’s ratio affected by temperature?
Solution:
In general, lower temperatures reduce both horizontal and vertical strain, while higher temperatures increase both horizontal and vertical strain. As a result, the net effect on Poisson’s Ratio is negligible because both horizontal and vertical strain change by the same amount.
Problem 4: A 2.0 m long metal wire is loaded, resulting in a 4 mm elongation. Find the change in diameter of wire when elongated if the diameter of wire is 1.5 mm and the Poisson’s ratio of wire is 0.24.
Solution:
Given:
Length of wire, L is 2.0 m.
Change in length, ΔL is 4 mm = 0.004 m
Diameter of wire, D is 1.5 mm.
Poisson’s ratio, ν is 0.24.
The longitudinal strain in the wire is given as:
Longitudinal strain = ΔL/L
= 0.004/2.0
= 0.002
The Poisson’s Ratio formula is as follows:
ν = Lateral strain/longitudinal strain
Substitute the given values to find the lateral strain.
0.24 = lateral strain / 0.002
Lateral strain = 0.00048
The lateral strain in a wire is given as:
Lateral strain = ΔD / D
0.00048 = ΔD / 1.5 mm
ΔD = 0.00072 mm
Hence, the change in diameter of the wire is 0.00072 mm.
Problem 5: What if a material’s Poisson ratio is zero?
Solution:
A Poisson’s ratio of 0 indicates that the material does not deform in either the lateral or axial directions in response to the application of force. Cork is an example of a material with a Poisson’s ratio of nearly 0 and no deformation under stress. Cork is applied as a seal in bottle stoppers because it expands and contracts under stress, protecting the substance inside.
FAQs on Poisson’s Ratio
What is Poisson’s Ratio?
Poisson Ratio is the negative of the ratio of lateral strain to the longitudinal strain.
What is the Formula for Poisson’s Ratio?
The formula for Poisson’s Ratio is given as
Poisson’s Ratio = – Transversal Strain/Longitudinal Strain
What is the Unit of Poisson’s Ratio?
Poisson’s Ratio has no units. It is a unitless scalar quantity.
What is Poisson’s Ratio of Steel?
The value of Poisson’s Ratio of Steel is 0.28.
What is Poisson’s Ratio of Concrete?
The value of Poisson’s Ratio of Concrete is 0.1 to 0.2.
Why is Poisson’s Ratio Negative?
The negative sign in the formula of Poisson’s Ratio is to make the ratio of transversal strain to the longitudinal strain positive.
Which Material has the Highest Poisson Ratio?
Elastic Rubber has the highest Poisson’s Ratio.
What does Poisson’s Ratio 0.5 signify?
The value of Poisson’s Ratio 0.5 signify that the material is incompressible but deformed within elastic limits.
Why Poisson’s Ratio of Cork is Zero?
The Zero value of Poisson’s Ratio of a Cork is because there is no deformation either in longitudinal or lateral direction on application of stress.
What is Poisson’s Ratio of Rubber?
Rubber has approximate Poisson’s Ratio of 0.5.
What is Poisson’s Ratio of Soil?
As soil is not same everywhere, for soft to stiff clay Poisson’s ratio fof 0.20–0.45 and for loose sand Poisson’s ratio is 0.15–0.35.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...