Plot Z-Score in R
Last Updated :
29 Feb, 2024
R supports powerful tools to plot z-score according to a given p-value. Thus, to learn about the z score we should know about the p-value. p-value and z scores are called statistical parameters and are used to make statistical calculations.
p-value is the probability of obtaining results at least as extreme as the observed result. Just like probability p-values lie between 0 and 1. If the Null hypothesis of a study comes out to be true then the p-value or calculated probability is the probability of finding the more extreme results.
z-score describes a value’s relationship to the mean of the group values. Let us take an example to understand the concept of z-score properly:
Consider a case of a class of 25 students. After the exams, the mean score of the class comes out to be 45. If we want to know whether a person who has scored 75 marks in the exam is among 10% of the scorers. In starting, it may seem to be a very tedious calculation. But by knowing the concept of z-scores it can become fairly easy.
The formula for calculating z-score:
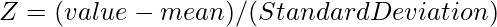
- Standard deviation means how far the result is from the average value.
- Now a z score of 1 denotes that the observation is at a distance of one standard deviation towards right from the center.
- Similarly, a z score of -1 tells us that the observation is one standard deviation left from the center.
Method 1: Naive approach
Approach:
- Create a vector and assign various values to it.
- Find the mean of the vector using function mean().
- Find the standard deviation using function sd().
- Subtract the mean value from the observation and divide the resultant with standard deviation.
- The vector obtained will have the required Z-score values.
- Now simply plot it.
Example 1:
R
a <- c(9, 10, 12, 14, 5, 8, 9)
mean(a)
sd(a)
a.z <- (a - mean(a)) / sd(a)
plot(a.z, type="o", col="green")
|
Output:

Example 2:
R
a <- c(7, 9, 2, 4, 25, 18, 19)
mean(a)
sd(a)
a.z <- (a - mean(a)) / sd(a)
plot(a.z, type="o", col="green")
|
Output:

Method 2: Using qnorm()
If we are given a p-value and our value is 0.70 then this means that it will be a point below which there are 80% of observations and 20% of observations lie above it. The easiest way for finding a z score if a p-value is given is to use qnorm() function. It takes the p-value as an argument and gives the z score as output.
Syntax:
qnorm(p-value)
Approach:
- Call qnorm() function with required p-value
- Plot z-score with the value so obtained
Example :
R
set <- qnorm(0.75)
plot(set, type="o", col="green")
|
Output:

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...