Persistent data structures
Last Updated :
28 Feb, 2024
All the data structures discussed here so far are non-persistent (or ephemeral). A persistent data structure is a data structure that always preserves the previous version of itself when it is modified. They can be considered as ‘immutable’ as updates are not in-place. A data structure is partially persistent if all versions can be accessed but only the newest version can be modified. Fully persistent if every version can be both accessed and modified. Confluently persistent is when we merge two or more versions to get a new version. This induces a DAG on the version graph. Persistence can be achieved by simply copying, but this is inefficient in CPU and RAM usage as most operations will make only a small change in the DS. Therefore, a better method is to exploit the similarity between the new and old versions to share structure between them.
Examples:
- Linked List Concatenation : Consider the problem of concatenating two singly linked lists with n and m as the number of nodes in them. Say n>m. We need to keep the versions, i.e., we should be able to original list. One way is to make a copy of every node and do the connections. O(n + m) for traversal of lists and O(1) each for adding (n + m – 1) connections. Other way, and a more efficient way in time and space, involves traversal of only one of the two lists and fewer new connections. Since we assume m<n, we can pick list with m nodes to be copied. This means O(m) for traversal and O(1) for each one of the (m) connections. We must copy it otherwise the original form of list wouldn’t have persisted.
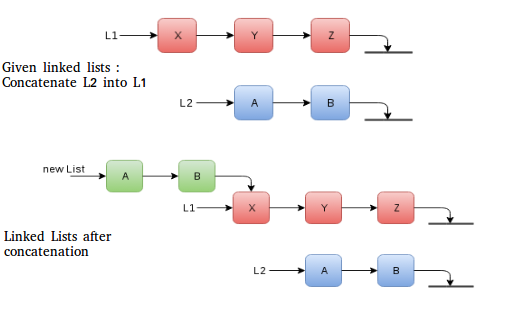
Pseudo code to implement it:
LinkedList concatenate(LinkedList list1, LinkedList list2) {
Node *current = list1.head;
while (current->next != nullptr) {
current = current->next;
}
current->next = list2.head;
list1.tail = list2.tail;
return list1;
}
Explanation:
In this code, LinkedList represents a linked list, and Node represents a node in the linked list. The concatenate function takes two linked lists as input and concatenates them by modifying the next pointer of the last node of the first linked list to point to the head of the second linked list. The tail of the first linked list is then set to the tail of the second linked list. Finally, the modified first linked list is returned.
- Binary Search Tree Insertion : Consider the problem of insertion of a new node in a binary search tree. Being a binary search tree, there is a specific location where the new node will be placed. All the nodes in the path from the new node to the root of the BST will observe a change in structure (cascading). For example, the node for which the new node is the child will now have a new pointer. This change in structure induces change in the complete path up to the root. Consider tree below with value for node listed inside each one of them.

Pseudo code to implement it:
class Node {
int key;
Node *left, *right;
};
class BST {
public:
Node *root;
BST() {
root = nullptr;
}
Node *createNode(int key) {
Node *newNode = new Node;
newNode->key = key;
newNode->left = newNode->right = nullptr;
return newNode;
}
Node *insert(Node *root, int key) {
if (root == nullptr)
return createNode(key);
if (key < root->key)
root->left = insert(root->left, key);
else if (key > root->key)
root->right = insert(root->right, key);
return root;
}
Node *copyTree(Node *root) {
if (root == nullptr)
return nullptr;
Node *newNode = createNode(root->key);
newNode->left = copyTree(root->left);
newNode->right = copyTree(root->right);
return newNode;
}
BST makePersistent(int key) {
BST newBST;
newBST.root = copyTree(root);
newBST.root = newBST.insert(newBST.root, key);
return newBST;
}
};
int main() {
BST bst1;
bst1.root = bst1.insert(bst1.root, 50);
bst1.root = bst1.insert(bst1.root, 30);
bst1.root = bst1.insert(bst1.root, 20);
bst1.root = bst1.insert(bst1.root, 40);
bst1.root = bst1.insert(bst1.root, 70);
bst1.root = bst1.insert(bst1.root, 60);
bst1.root = bst1.insert(bst1.root, 80);
BST bst2 = bst1.makePersistent(55);
// bst1 remains unchanged
// bst2 has a new node with key 55
return 0;
}
Below is the implementation of the above approach:
C++
#include<iostream>
class Node {
public:
int key;
Node *left, *right;
};
class BST {
public:
Node *root;
BST() {
root = nullptr;
}
Node *createNode(int key) {
Node *newNode = new Node;
newNode->key = key;
newNode->left = newNode->right = nullptr;
return newNode;
}
Node *insert(Node *root, int key) {
if (root == nullptr)
return createNode(key);
if (key < root->key)
root->left = insert(root->left, key);
else if (key > root->key)
root->right = insert(root->right, key);
return root;
}
Node *copyTree(Node *root) {
if (root == nullptr)
return nullptr;
Node *newNode = createNode(root->key);
newNode->left = copyTree(root->left);
newNode->right = copyTree(root->right);
return newNode;
}
BST makePersistent(int key) {
BST newBST;
newBST.root = copyTree(root);
newBST.root = newBST.insert(newBST.root, key);
return newBST;
}
void printInOrder(Node *root) {
if (root != nullptr) {
printInOrder(root->left);
std::cout << root->key << " ";
printInOrder(root->right);
}
}
};
int main() {
BST bst1;
bst1.root = bst1.insert(bst1.root, 50);
bst1.root = bst1.insert(bst1.root, 30);
bst1.root = bst1.insert(bst1.root, 20);
bst1.root = bst1.insert(bst1.root, 40);
bst1.root = bst1.insert(bst1.root, 70);
bst1.root = bst1.insert(bst1.root, 60);
bst1.root = bst1.insert(bst1.root, 80);
BST bst2 = bst1.makePersistent(55);
std::cout << "BST1: ";
bst1.printInOrder(bst1.root);
std::cout << std::endl;
std::cout << "BST2: ";
bst2.printInOrder(bst2.root);
std::cout << std::endl;
return 0;
}
|
Java
import java.util.*;
class Node {
public int key;
public Node left, right;
public Node(int item) {
key = item;
left = right = null;
}
}
class BST {
public Node root;
public BST() {
root = null;
}
public void insert(int key) {
root = insertRec(root, key);
}
public Node insertRec(Node root, int key) {
if (root == null) {
root = new Node(key);
return root;
}
if (key < root.key)
root.left = insertRec(root.left, key);
else if (key > root.key)
root.right = insertRec(root.right, key);
return root;
}
public Node copyTree(Node root) {
if (root == null)
return null;
Node newNode = new Node(root.key);
newNode.left = copyTree(root.left);
newNode.right = copyTree(root.right);
return newNode;
}
public BST makePersistent(int key) {
BST newBST = new BST();
newBST.root = copyTree(root);
newBST.insert(key);
return newBST;
}
public void printInOrder(Node root) {
if (root != null) {
printInOrder(root.left);
System.out.print(root.key + " ");
printInOrder(root.right);
}
}
}
public class Main {
public static void main(String[] args) {
BST bst1 = new BST();
bst1.insert(50);
bst1.insert(30);
bst1.insert(20);
bst1.insert(40);
bst1.insert(70);
bst1.insert(60);
bst1.insert(80);
BST bst2 = bst1.makePersistent(55);
System.out.print("BST1: ");
bst1.printInOrder(bst1.root);
System.out.println();
System.out.print("BST2: ");
bst2.printInOrder(bst2.root);
System.out.println();
}
}
|
Python3
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
class BST:
def __init__(self):
self.root = None
def create_node(self, key):
return Node(key)
def insert(self, root, key):
if root is None:
return self.create_node(key)
if key < root.key:
root.left = self.insert(root.left, key)
elif key > root.key:
root.right = self.insert(root.right, key)
return root
def copy_tree(self, root):
if root is None:
return None
new_node = self.create_node(root.key)
new_node.left = self.copy_tree(root.left)
new_node.right = self.copy_tree(root.right)
return new_node
def make_persistent(self, key):
new_bst = BST()
new_bst.root = self.copy_tree(self.root)
new_bst.root = new_bst.insert(new_bst.root, key)
return new_bst
def print_in_order(self, root):
if root is not None:
self.print_in_order(root.left)
print(root.key, end=" ")
self.print_in_order(root.right)
if __name__ == "__main__":
bst1 = BST()
bst1.root = bst1.insert(bst1.root, 50)
bst1.root = bst1.insert(bst1.root, 30)
bst1.root = bst1.insert(bst1.root, 20)
bst1.root = bst1.insert(bst1.root, 40)
bst1.root = bst1.insert(bst1.root, 70)
bst1.root = bst1.insert(bst1.root, 60)
bst1.root = bst1.insert(bst1.root, 80)
bst2 = bst1.make_persistent(55)
print("BST1: ", end="")
bst1.print_in_order(bst1.root)
print()
print("BST2: ", end="")
bst2.print_in_order(bst2.root)
print()
|
C#
using System;
public class Node {
public int key;
public Node left, right;
};
public class BST {
public Node root;
public BST() {
root = null;
}
public Node createNode(int key) {
Node newNode = new Node();
newNode.key = key;
newNode.left = newNode.right = null;
return newNode;
}
public Node insert(Node root, int key) {
if (root == null)
return createNode(key);
if (key < root.key)
root.left = insert(root.left, key);
else if (key > root.key)
root.right = insert(root.right, key);
return root;
}
public Node copyTree(Node root) {
if (root == null)
return null;
Node newNode = createNode(root.key);
newNode.left = copyTree(root.left);
newNode.right = copyTree(root.right);
return newNode;
}
public BST makePersistent(int key) {
BST newBST = new BST();
newBST.root = copyTree(root);
newBST.root = newBST.insert(newBST.root, key);
return newBST;
}
public void printInOrder(Node root) {
if (root != null) {
printInOrder(root.left);
Console.Write(root.key + " ");
printInOrder(root.right);
}
}
};
public class Program {
public static void Main() {
BST bst1 = new BST();
bst1.root = bst1.insert(bst1.root, 50);
bst1.root = bst1.insert(bst1.root, 30);
bst1.root = bst1.insert(bst1.root, 20);
bst1.root = bst1.insert(bst1.root, 40);
bst1.root = bst1.insert(bst1.root, 70);
bst1.root = bst1.insert(bst1.root, 60);
bst1.root = bst1.insert(bst1.root, 80);
BST bst2 = bst1.makePersistent(55);
Console.Write("BST1: ");
bst1.printInOrder(bst1.root);
Console.WriteLine();
Console.Write("BST2: ");
bst2.printInOrder(bst2.root);
Console.WriteLine();
}
}
|
Javascript
class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
}
class BST {
constructor() {
this.root = null;
}
insert(root, key) {
if (root === null) {
return new Node(key);
}
if (key < root.key) {
root.left = this.insert(root.left, key);
} else if (key > root.key) {
root.right = this.insert(root.right, key);
}
return root;
}
copyTree(root) {
if (root === null) {
return null;
}
const newNode = new Node(root.key);
newNode.left = this.copyTree(root.left);
newNode.right = this.copyTree(root.right);
return newNode;
}
makePersistent(key) {
const newBST = new BST();
newBST.root = this.copyTree(this.root);
newBST.root = newBST.insert(newBST.root, key);
return newBST;
}
printInOrder(root) {
if (root !== null) {
this.printInOrder(root.left);
console.log(root.key + " ");
this.printInOrder(root.right);
}
}
}
const bst1 = new BST();
bst1.root = bst1.insert(bst1.root, 50);
bst1.root = bst1.insert(bst1.root, 30);
bst1.root = bst1.insert(bst1.root, 20);
bst1.root = bst1.insert(bst1.root, 40);
bst1.root = bst1.insert(bst1.root, 70);
bst1.root = bst1.insert(bst1.root, 60);
bst1.root = bst1.insert(bst1.root, 80);
const bst2 = bst1.makePersistent(55);
console.log("BST1: ");
bst1.printInOrder(bst1.root);
console.log("");
console.log("BST2: ");
bst2.printInOrder(bst2.root);
console.log("");
|
Output
BST1: 20 30 40 50 60 70 80
BST2: 20 30 40 50 55 60 70 80
Explanation –
In this code, the Node structure represents a node in the binary search tree, and the BST class implements a binary search tree. The createNode function creates a new node with the given key, the insert function inserts a new key into the tree, and the copyTree function creates a copy of the binary search tree. The makePersistent function creates a new persistent version of the binary search tree by copying the existing tree and inserting a new key into the copy.
This algorithm creates a new version of the binary search tree whenever a modification is made to it, so that each version of the tree is stored in its entirety. This approach is memory-inefficient, as multiple versions of the tree are kept in memory, but it ensures that each version of the tree remains unchanged and can be used for reading.
Approaches to make data structures persistent For the methods suggested below, updates and access time and space of versions vary with whether we are implementing full or partial persistence.
- Path copying: Make a copy of the node we are about to update. Then proceed for update. And finally, cascade the change back through the data structure, something very similar to what we did in example two above. This causes a chain of updates, until you reach a node no other node points to — the root. How to access the state at time t? Maintain an array of roots indexed by timestamp.
- Fat nodes: As the name suggests, we make every node store its modification history, thereby making it ‘fat’.
- Nodes with boxes: Amortized O(1) time and space can be achieved for access and updates. This method was given by Sleator, Tarjan and their team. For a tree, it involves using a modification box that can hold: a. one modification to the node (the modification could be of one of the pointers, or to the node’s key or to some other node-specific data) b. the time when the mod was applied The timestamp is crucial for reaching to the version of the node we care about. One can read more about it here. With this algorithm, given any time t, at most one modification box exists in the data structure with time t. Thus, a modification at time t splits the tree into three parts: one part contains the data from before time t, one part contains the data from after time t, and one part was unaffected by the modification (Source: MIT OCW ). Non-tree data structures may require more than one modification box, but limited to in-degree of the node for amortized O(1).
- Copy-on-write: This approach creates a new version of the data structure whenever a modification is made to it. The old version is still available for reading, while the new version is used for writes. This approach is memory-efficient, as most of the time, only one version of the data structure is active.
- Snapshotting: This approach involves taking a snapshot of the data structure at a particular moment in time and then storing the snapshot. The snapshots can be used for reading, and modifications can be made to the latest snapshot. This approach is simple to implement but can be memory-inefficient as multiple snapshots of the data structure are kept in memory.
- Persistent arrays: This approach involves creating a new version of the data structure whenever a modification is made to it, but only modifying the elements that have changed. The rest of the elements are shared between the different versions. This approach is memory-efficient but can be complex to implement.
- Path copying: This approach involves creating a new version of the data structure whenever a modification is made to it, but only copying the portion of the data structure that has changed. This approach is memory-efficient and can be simple to implement, but it may result in long chains of small updates that can slow down the system.
- Log-structured data structures: This approach involves logging all modifications made to the data structure, and using the log to recreate the data structure at a later time. This approach is memory-efficient, but it can be complex to implement and may result in slow updates.
These are some of the most common approaches to make data structures persistent, but the specific approach to use depends on the requirements and constraints of the system.
Useful Links:
- MIT OCW (Erik Demaine)
- MIT OCW (David Karger)
- Dann Toliver’s talk
- Wiki Page
Persistent Segment Tree | Set 1 (Introduction)
Share your thoughts in the comments
Please Login to comment...