Pernicious number
Last Updated :
15 Jun, 2022
A pernicious number is a positive integer which has prime number of ones in its binary representation. The first pernicious number is 3 since 3 = (11)(in binary representation) and 1 + 1 = 2, which is a prime.
Properties of Pernicious Numbers :
1. There isn’t any pernicious number which is also power of 2 because powers of two in binary form are represented as a one followed by zeros. So, 1 is not considered as a prime number.
2. Every number of the form 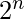 + 1 with n > 0 is a pernicious number as the number of ones in binary form is 2 which is prime.
+ 1 with n > 0 is a pernicious number as the number of ones in binary form is 2 which is prime.
3. A number of the form 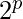 – 1 with prime p is a pernicious number known as a Mersenne number .
– 1 with prime p is a pernicious number known as a Mersenne number .
The idea to print first n Pernicious numbers is simple.
Do following for every number from 1 to n.
1) Count set bits in current number
2) Print current number if count of set bits is prime. We use simple primality check for this purpose.
Here is the program to print first 25 pernicious number.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
bool isPrime(int x)
{
if (x < 2)
return false;
for (int i = 2; i < x; i++) {
if (x % i == 0)
return false;
}
return true;
}
void printPernicious(int n)
{
for (int i=1,count=0; count<n; i++) {
if (isPrime(__builtin_popcount(i))) {
cout << i << " ";
count++;
}
}
}
int main()
{
int n = 25;
printPernicious(n);
return 0;
}
|
Java
import java.util.*;
class GFG {
static int countSetBits(int n)
{
int count = 0;
while (n > 0)
{
n &= (n - 1) ;
count++;
}
return count;
}
static boolean isPrime(int x)
{
if (x < 2)
return false;
for (int i = 2; i < x; i++) {
if (x % i == 0)
return false;
}
return true;
}
static void printPernicious(int n)
{
for (int i=1,count=0; count<n; i++) {
if (isPrime(countSetBits(i))) {
System.out.print( i + " ");
count++;
}
}
}
public static void main (String[] args) {
int n = 25;
printPernicious(n);
}
}
|
Python3
def isPrime(x):
if x < 2:
return False
for i in range(2, x):
if not x % i:
return False
return True
def printPernicious(n):
i, count = 1, 0
while count < n:
if (isPrime(bin(i).count('1'))):
print(i, end=' ')
count += 1
i += 1
n = 25
printPernicious(n)
|
C#
using System;
class GFG
{
static int countSetBits(int n)
{
int count = 0;
while (n > 0)
{
n &= (n - 1) ;
count++;
}
return count;
}
static bool isPrime(int x)
{
if (x < 2)
return false;
for (int i = 2; i < x; i++) {
if (x % i == 0)
return false;
}
return true;
}
static void printPernicious(int n)
{
for (int i=1,count=0; count<n; i++) {
if (isPrime(countSetBits(i))) {
Console.Write( i + " ");
count++;
}
}
}
public static void Main ()
{
int n = 25;
printPernicious(n);
}
}
|
PHP
<?php
function isPrime($x)
{
if ($x < 2)
return false;
for ($i = 2; $i < $x; $i++)
{
if ($x % $i == 0)
return false;
}
return true;
}
function getBitCount($value)
{
$count = 0;
while($value)
{
$count += ($value & 1);
$value = $value >> 1;
}
return $count;
}
function printPernicious($n)
{
for ($i = 1, $count = 0;
$count < $n; $i++)
{
if (isPrime(getBitCount($i)))
{
echo $i." ";
$count++;
}
}
}
$n = 25;
printPernicious($n);
?>
|
Javascript
<script>
function countSetBits(n)
{
let count = 0;
while (n > 0)
{
n &= (n - 1) ;
count++;
}
return count;
}
function isPrime(x)
{
if (x < 2)
return false;
for (let i = 2; i < x; i++) {
if (x % i == 0)
return false;
}
return true;
}
function printPernicious(n)
{
for (let i=1,count=0; count<n; i++) {
if (isPrime(countSetBits(i))) {
document.write( i + " ");
count++;
}
}
}
let n = 25;
printPernicious(n);
</script>
|
Output :
3 5 6 7 9 10 11 12 13 14 17 18 19 20 21 22 24 25 26 28 31 33 34 35 36
Time Complexity: O(nlogn)
Space Complexity: O(1)
References :
Wiki
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...