Permutation Groups and Multiplication of Permutation
Last Updated :
18 May, 2022
Let G be a non-empty set, then a one-one onto mapping to itself that is as shown below is called a permutation.

- The number of elements in finite set G is called the degree of Permutation.
- Let G have n elements then Pn is called a set of all permutations of degree n.
- Pn is also called the Symmetric group of degree n.
- Pn is also denoted by Sn.
- The number of elements in Pn or Sn is
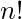
Examples:
Case1: Let G={ 1 } element then permutation are Sn or Pn = 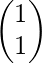
Case 2: Let G= { 1, 2 } elements then permutations are 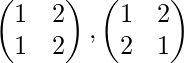
Case 3: Let G={ 1, 2, 3 } elements then permutation are 3!=6. These are,
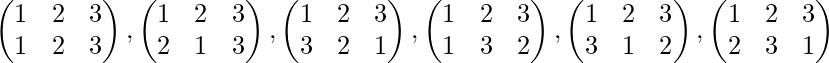
Reading the Symbol of Permutation
Suppose that a permutation is 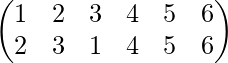
- First, we see that in a small bracket there are two rows written, these two rows have numbers. The smallest number is 1 and the largest number is 6.
- Starting from the left side of the first row we read as an image of 1 is 2, an image of 1 is 2, an image of 2 is 3, an image of 3 is 1, an image of 4 is 4 (Self image=identical=identity), an image of 5 is 6 and image of 6 is 5.
- The above thing can be also read as: Starting from the left side of the first row 1 goes to 2, 2goes to 3, 3goes to,4 goes to 4,5 goes to 6, and 6 goes to 5.
A cycle of length 2 is called a permutation.
Example:
1) 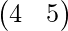
Length is 2, so it is a transposition.
2) 
Length is three, so it is not a transposition.
Multiplication of Permutation
Problem: If 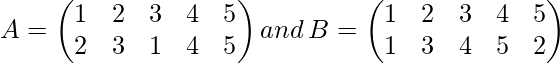
Find the product of permutation A.B and B.A
Solution: 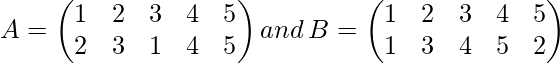

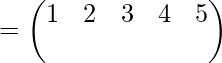
Here we can see that in first bracket 1 goes to 2 i.e. image of 1 is 2, and in second row 2 goes to 3 i.e. image of 2 is 3.
Hence, we will write 3 under 1 in the bracket shown below,
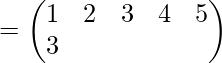
Do above step with all elements of first row, answer will be
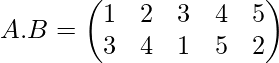
Similarly,
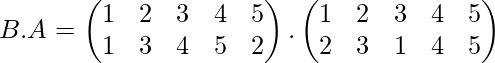
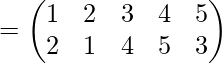
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...