Permutation refers to the process of arranging all the members of a given set to form a sequence. The number of permutations on a set of n elements is given by n! , where “!” represents factorial.
The Permutation Coefficient represented by P(n, k) is used to represent the number of ways to obtain an ordered subset having k elements from a set of n elements.
Mathematically it’s given as:
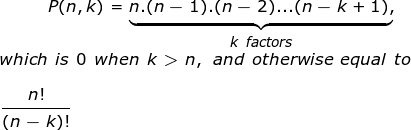
Image Source : Wiki
Examples :
P(10, 2) = 90
P(10, 3) = 720
P(10, 0) = 1
P(10, 1) = 10
The coefficient can also be computed recursively using the below recursive formula:
P(n, k) = P(n-1, k) + k* P(n-1, k-1)
The recursive formula for permutation-coefficient is :
P(n, k) = P(n-1, k) + k* P(n-1, k-1)
But how ??
here is the proof,
We already know,
The binomial coefficient is nCk = n!
k! (n-k)!
and, permutation-coefficient nPr = n!
(n-k)!
So, I can write
nCk = nPk
k!
=> k! * nCk = nPk ———————- eq.1
The recursive formula for the Binomial coefficient nCk can be written as,
nCk(n,k) = nCk(n-1,k-1) + nCk(n-1,k) you can refer to the following article for more details
https://www.geeksforgeeks.org/binomial-coefficient-dp-9/
Basically, it makes use of Pascal’s triangle which states that in order to fill the value at nCk[n][k] you need the summation of nCk[n-1][k-1] and nCk[n-1][k] along with some base cases. i.e,
nCk[n][k] = nCk[n-1][k-1]+nCk[n-1][k].
nCk[n][0] = nCk[n][n] = 1 (Base Case)
Anyways, let’s proceed with our eq.1
=> k! * nCk = nPk
=> k! * ( nCk(n-1,k-1) + nCk(n-1,k) ) = nPk [ as, nCk = nCk(n-1,k-1)+nCk(n-1,k) ]
=> k! * ( (n-1)! + (n-1)! ) = nPk
((n-1)-(k-1))! * (k-1)! (n-1-k)! * k!
=> k! * (n-1)! + k! * (n-1)! = nPk
((n-1)-(k-1))! * (k-1)! (n-1-k)! * k!
=> k * (k-1)! * (n-1)! + k! * (n-1)! = nPk [ as, k! = k*(k-1)! ]
((n-1)-(k-1))! * (k-1)! (n-1-k)! * k!
=> k * (n-1)! + (n-1)! = nPk
((n-1)-(k-1))! (n-1-k)!
(n-1)! can be replaced by nPk(n-1,k-1) as per the permutation-coefficient
((n-1) – (k-1))!
Similarly, (n-1)! can be replaced by nPk(n-1,k).
(n-1-k)!
Therefore,
=> k * nPk(n-1, k-1) + nPk(n-1, k) = nPk
Finally, that is where our recursive formula came from.
P(n, k) = P(n-1, k) + k* P(n-1, k-1)
If we observe closely, we can analyze that the problem has an overlapping substructure, hence we can apply dynamic programming here. Below is a program implementing the same idea.
C++
#include <bits/stdc++.h>
using namespace std;
#include<bits/stdc++.h>
int permutationCoeff(int n, int k)
{
int P[n + 1][k + 1];
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= std::min(i, k); j++)
{
if (j == 0)
P[i][j] = 1;
else
P[i][j] = P[i - 1][j] +
(j * P[i - 1][j - 1]);
P[i][j + 1] = 0;
}
}
return P[n][k];
}
int main()
{
int n = 10, k = 2;
cout << "Value of P(" << n <<" " << k<< ") is " << permutationCoeff(n, k);
return 0;
}
|
C
#include<bits/stdc++.h>
int permutationCoeff(int n, int k)
{
int P[n + 1][k + 1];
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= std::min(i, k); j++)
{
if (j == 0)
P[i][j] = 1;
else
P[i][j] = P[i - 1][j] +
(j * P[i - 1][j - 1]);
P[i][j + 1] = 0;
}
}
return P[n][k];
}
int main()
{
int n = 10, k = 2;
printf("Value of P(%d, %d) is %d ",
n, k, permutationCoeff(n, k));
return 0;
}
|
Java
import java.io.*;
import java.math.*;
class GFG
{
static int permutationCoeff(int n,
int k)
{
int P[][] = new int[n + 2][k + 2];
for (int i = 0; i <= n; i++)
{
for (int j = 0;
j <= Math.min(i, k);
j++)
{
if (j == 0)
P[i][j] = 1;
else
P[i][j] = P[i - 1][j] +
(j * P[i - 1][j - 1]);
P[i][j + 1] = 0;
}
}
return P[n][k];
}
public static void main(String args[])
{
int n = 10, k = 2;
System.out.println("Value of P( " + n + ","+ k +")" +
" is " + permutationCoeff(n, k) );
}
}
|
Python3
def permutationCoeff(n, k):
P = [[0 for i in range(k + 1)]
for j in range(n + 1)]
for i in range(n + 1):
for j in range(min(i, k) + 1):
if (j == 0):
P[i][j] = 1
else:
P[i][j] = P[i - 1][j] + (
j * P[i - 1][j - 1])
if (j < k):
P[i][j + 1] = 0
return P[n][k]
n = 10
k = 2
print("Value of P(", n, ", ", k, ") is ",
permutationCoeff(n, k), sep = "")
|
C#
using System;
class GFG
{
static int permutationCoeff(int n,
int k)
{
int [,]P = new int[n + 2,k + 2];
for (int i = 0; i <= n; i++)
{
for (int j = 0;
j <= Math.Min(i, k);
j++)
{
if (j == 0)
P[i,j] = 1;
else
P[i,j] = P[i - 1,j] +
(j * P[i - 1,j - 1]);
P[i,j + 1] = 0;
}
}
return P[n,k];
}
public static void Main()
{
int n = 10, k = 2;
Console.WriteLine("Value of P( " + n +
","+ k +")" + " is " +
permutationCoeff(n, k) );
}
}
|
PHP
<?php
function permutationCoeff( $n, $k)
{
$P = array(array());
for($i = 0; $i <= $n; $i++)
{
for($j = 0; $j <= min($i, $k); $j++)
{
if ($j == 0)
$P[$i][$j] = 1;
else
$P[$i][$j] = $P[$i - 1][$j] +
($j * $P[$i - 1][$j - 1]);
$P[$i][$j + 1] = 0;
}
}
return $P[$n][$k];
}
$n = 10; $k = 2;
echo "Value of P(",$n," ,",$k,") is ",
permutationCoeff($n, $k);
?>
|
Javascript
<script>
function permutationCoeff(n, k)
{
let P = new Array(n + 2);
for(let i = 0; i < n + 2; i++)
{
P[i] = new Array(k + 2);
}
for (let i = 0; i <= n; i++)
{
for (let j = 0; j <= Math.min(i, k); j++)
{
if (j == 0)
P[i][j] = 1;
else
P[i][j] = P[i - 1][j] + (j * P[i - 1][j - 1]);
P[i][j + 1] = 0;
}
}
return P[n][k];
}
let n = 10, k = 2;
document.write("Value of P(" + n + ","+ k +")" + " is " + permutationCoeff(n, k) );
</script>
|
Output :
Value of P(10, 2) is 90
Here as we can see the time complexity is O(n*k) and space complexity is O(n*k) as the program uses an auxiliary matrix to store the result.
Can we do it in O(n) time ?
Let us suppose we maintain a single 1D array to compute the factorials up to n. We can use computed factorial value and apply the formula P(n, k) = n! / (n-k)!. Below is a program illustrating the same concept.
C++
#include<bits/stdc++.h>
using namespace std;
int permutationCoeff(int n, int k)
{
int fact[n + 1];
fact[0] = 1;
for(int i = 1; i <= n; i++)
fact[i] = i * fact[i - 1];
return fact[n] / fact[n - k];
}
int main()
{
int n = 10, k = 2;
cout << "Value of P(" << n << ", "
<< k << ") is "
<< permutationCoeff(n, k);
return 0;
}
|
C
#include<bits/stdc++.h>
int permutationCoeff(int n, int k)
{
int fact[n + 1];
fact[0] = 1;
for (int i = 1; i <= n; i++)
fact[i] = i * fact[i - 1];
return fact[n] / fact[n - k];
}
int main()
{
int n = 10, k = 2;
printf ("Value of P(%d, %d) is %d ",
n, k, permutationCoeff(n, k) );
return 0;
}
|
Java
import java .io.*;
public class GFG {
static int permutationCoeff(int n,
int k)
{
int []fact = new int[n+1];
fact[0] = 1;
for (int i = 1; i <= n; i++)
fact[i] = i * fact[i - 1];
return fact[n] / fact[n - k];
}
static public void main (String[] args)
{
int n = 10, k = 2;
System.out.println("Value of"
+ " P( " + n + ", " + k + ") is "
+ permutationCoeff(n, k) );
}
}
|
Python3
def permutationCoeff(n, k):
fact = [0 for i in range(n + 1)]
fact[0] = 1
for i in range(1, n + 1):
fact[i] = i * fact[i - 1]
return int(fact[n] / fact[n - k])
n = 10
k = 2
print("Value of P(", n, ", ", k, ") is ",
permutationCoeff(n, k), sep = "")
|
C#
using System;
public class GFG {
static int permutationCoeff(int n,
int k)
{
int []fact = new int[n+1];
fact[0] = 1;
for (int i = 1; i <= n; i++)
fact[i] = i * fact[i - 1];
return fact[n] / fact[n - k];
}
static public void Main ()
{
int n = 10, k = 2;
Console.WriteLine("Value of"
+ " P( " + n + ", " + k + ") is "
+ permutationCoeff(n, k) );
}
}
|
PHP
<?php
function permutationCoeff($n, $k)
{
$fact = array();
$fact[0] = 1;
for ($i = 1; $i <= $n; $i++)
$fact[$i] = $i * $fact[$i - 1];
return $fact[$n] / $fact[$n - $k];
}
$n = 10;
$k = 2;
echo"Value of P(",$n," ", $k,") is ",
permutationCoeff($n, $k) ;
?>
|
Javascript
<script>
function permutationCoeff(n, k)
{
let fact = new Array(n+1);
fact[0] = 1;
for (let i = 1; i <= n; i++)
fact[i] = i * fact[i - 1];
return parseInt(fact[n] / fact[n - k], 10);
}
let n = 10, k = 2;
document.write("Value of"
+ " P(" + n + ", " + k + ") is "
+ permutationCoeff(n, k) );
</script>
|
Output :
Value of P(10, 2) is 90
A O(n) time and O(1) Extra Space Solution
C++
#include <iostream>
using namespace std;
int PermutationCoeff(int n, int k)
{
int P = 1;
for (int i = 0; i < k; i++)
P *= (n-i) ;
return P;
}
int main()
{
int n = 10, k = 2;
cout << "Value of P(" << n << ", " << k
<< ") is " << PermutationCoeff(n, k);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int PermutationCoeff(int n,
int k)
{
int Fn = 1, Fk = 1;
for (int i = 1; i <= n; i++)
{
Fn *= i;
if (i == n - k)
Fk = Fn;
}
int coeff = Fn / Fk;
return coeff;
}
public static void main(String args[])
{
int n = 10, k = 2;
System.out.println("Value of P( " + n + "," +
k +") is " +
PermutationCoeff(n, k) );
}
}
|
C#
using System;
class GFG {
static int PermutationCoeff(int n,
int k)
{
int Fn = 1, Fk = 1;
for (int i = 1; i <= n; i++)
{
Fn *= i;
if (i == n - k)
Fk = Fn;
}
int coeff = Fn / Fk;
return coeff;
}
public static void Main()
{
int n = 10, k = 2;
Console.WriteLine("Value of P( "
+ n + "," + k +") is "
+ PermutationCoeff(n, k) );
}
}
|
PHP
<?php
function PermutationCoeff( $n, $k)
{
$Fn = 1; $Fk;
for ( $i = 1; $i <= $n; $i++)
{
$Fn *= $i;
if ($i == $n - $k)
$Fk = $Fn;
}
$coeff = $Fn / $Fk;
return $coeff;
}
$n = 10; $k = 2;
echo "Value of P(" , $n , ", " , $k , ")
is " , PermutationCoeff($n, $k);
?>
|
Javascript
<script>
function PermutationCoeff(n, k)
{
let P = 1;
for(let i = 0; i < k; i++)
P *= (n - i);
return P;
}
let n = 10, k = 2;
document.write("Value of P(" + n +
", " + k + ") is " +
PermutationCoeff(n, k));
</script>
|
Python3
def permutationCoeff(n, k):
f=1
for i in range(k):
f*=(n-i)
return f
n = 10
k = 2
print("Value of P(", n, ", ", k, ") is ",
permutationCoeff(n, k))
|
Output :
Value of P(10, 2) is 90
Thanks to Shiva Kumar for suggesting this solution.
This article is contributed by Ashutosh Kumar. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above