Perfect Square factors of a Number

Given an integer N, the task is to find the number of factors of N which are a perfect square.

Examples:

Input: N = 100 
Output: 4 
Explanation:
There are four factors of 
100 (1, 4, 25, 100) that are perfect square.
Input: N = 900 
Output: 8 
Explanation:
There are eight factors of 900 (1, 4, 9, 25, 36, 100, 225, 900) that are perfect square.  

Naive Approach: The simplest approach to solve this problem is to find all possible factors of the given number N and for each factor, check if the factor is a perfect square or not. For every factor found to be so, increase count. Print the final count. 
Time Complexity: O(N) 
Auxiliary Space: O(1)

Efficient Approach:
The following observations need to be made to optimize the above approach:
The number of factors for a number is given by:  

Factors of N = (1 + a₁)*(1 + a₂)*(1 + a₃)*..*(1 + a_n) 
where a₁, a₂, a₃, …, a_n are the count of distinct prime factors of N.  

In a perfect square, the count of distinct prime factors must be divisible by 2. Therefore, the count of factors that are a perfect square is given by:

Factors of N that are perfect square = (1 + a₁/2)*(1 + a₂/2)*…*(1 + a_n/2) where a₁, a₂, a₃, …, a_n are the count of distinct prime factors of N.  

Illustration:

The prime factors of N = 100 are 2, 2, 5, 5. 
Therefore, the number of factors that are perfect square are (1 + 2/2) * (1 + 2/2) = 4. 
The factors are 1, 4, 25, 100. 

Therefore, find the count of prime factors and apply the above formula to find the count of factors that are a perfect square.
Below is the implementation of the above approach:

C++

// C++ Program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;

// Function that returns the count of
// factors that are perfect squares
int noOfFactors(int N)
{
    if (N == 1)
        return 1;

    // Stores the count of number
    // of times a prime number
    // divides N.
    int count = 0;

    // Stores the number of factors
    // that are perfect square
    int ans = 1;

    // Count number of 2's
    // that divides N
    while (N % 2 == 0) {
        count++;
        N = N / 2;
    }

    // Calculate ans according
    // to above formula
    ans *= (count / 2 + 1);

    // Check for all the possible
    // numbers that can divide it
    for (int i = 3;
         i * i <= N; i = i + 2) {
        count = 0;

        // Check the number of
        // times prime number
        // i divides it
        while (N % i == 0) {
            count++;
            N = N / i;
        }

        // Calculate ans according
        // to above formula
        ans *= (count / 2 + 1);
    }

    // Return final count
    return ans;
}

// Driver Code
int main()
{
    int N = 100;

    cout << noOfFactors(N);

    return 0;
}

Java

// Java program to implement
// the above approach
import java.util.*;

class GFG{

// Function that returns the count of
// factors that are perfect squares
static int noOfFactors(int N)
{
    if (N == 1)
        return 1;

    // Stores the count of number
    // of times a prime number
    // divides N.
    int count = 0;

    // Stores the number of factors
    // that are perfect square
    int ans = 1;

    // Count number of 2's
    // that divides N
    while (N % 2 == 0)
    {
        count++;
        N = N / 2;
    }

    // Calculate ans according
    // to above formula
    ans *= (count / 2 + 1);

    // Check for all the possible
    // numbers that can divide it
    for(int i = 3; i * i <= N; i = i + 2)
    {
        count = 0;

        // Check the number of
        // times prime number
        // i divides it
        while (N % i == 0)
        {
            count++;
            N = N / i;
        }

        // Calculate ans according
        // to above formula
        ans *= (count / 2 + 1);
    }

    // Return final count
    return ans;
}

// Driver Code
public static void main(String[] args)
{
    int N = 100;

    System.out.print(noOfFactors(N));
}
}

// This code is contributed by 29AjayKumar

Python3

# Python3 program to implement
# the above approach

# Function that returns the count of
# factors that are perfect squares
def noOfFactors(N):

    if (N == 1):
        return 1

    # Stores the count of number
    # of times a prime number
    # divides N.
    count = 0

    # Stores the number of factors
    # that are perfect square
    ans = 1

    # Count number of 2's
    # that divides N
    while (N % 2 == 0):
        count += 1
        N = N // 2

    # Calculate ans according
    # to above formula
    ans *= (count // 2 + 1)

    # Check for all the possible
    # numbers that can divide it
    i = 3
    while i * i <= N:
        count = 0

        # Check the number of
        # times prime number
        # i divides it
        while (N % i == 0):
            count += 1
            N = N // i

        # Calculate ans according
        # to above formula
        ans *= (count // 2 + 1)
        i += 2

    # Return final count
    return ans

# Driver Code
if __name__ == "__main__":

    N = 100

    print(noOfFactors(N))

# This code is contributed by chitranayal

C#

// C# program to implement
// the above approach
using System;

class GFG{

// Function that returns the count of
// factors that are perfect squares
static int noOfFactors(int N)
{
    if (N == 1)
        return 1;

    // Stores the count of number
    // of times a prime number
    // divides N.
    int count = 0;

    // Stores the number of factors
    // that are perfect square
    int ans = 1;

    // Count number of 2's
    // that divides N
    while (N % 2 == 0)
    {
        count++;
        N = N / 2;
    }

    // Calculate ans according
    // to above formula
    ans *= (count / 2 + 1);

    // Check for all the possible
    // numbers that can divide it
    for(int i = 3; i * i <= N; i = i + 2)
    {
        count = 0;

        // Check the number of
        // times prime number
        // i divides it
        while (N % i == 0)
        {
            count++;
            N = N / i;
        }

        // Calculate ans according
        // to above formula
        ans *= (count / 2 + 1);
    }

    // Return final count
    return ans;
}

// Driver Code
public static void Main(String[] args)
{
    int N = 100;

    Console.Write(noOfFactors(N));
}
}

// This code is contributed by PrinciRaj1992

Javascript

<script>

// Javascript program for
// the above approach

// Function that returns the count of
// factors that are perfect squares
function noOfFactors(N)
{
    if (N == 1)
        return 1;

    // Stores the count of number
    // of times a prime number
    // divides N.
    let count = 0;

    // Stores the number of factors
    // that are perfect square
    let ans = 1;

    // Count number of 2's
    // that divides N
    while (N % 2 == 0)
    {
        count++;
        N = N / 2;
    }

    // Calculate ans according
    // to above formula
    ans *= (count / 2 + 1);

    // Check for all the possible
    // numbers that can divide it
    for(let i = 3; i * i <= N; i = i + 2)
    {
        count = 0;

        // Check the number of
        // times prime number
        // i divides it
        while (N % i == 0)
        {
            count++;
            N = N / i;
        }

        // Calculate ans according
        // to above formula
        ans *= (count / 2 + 1);
    }

    // Return final count
    return ans;
}

// Driver Code

   let N = 100;

  document.write(noOfFactors(N));

</script>

Output

4

Time Complexity: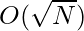 
Space Complexity: O(1)

Perfect Square factors of a Number using inbuilt function

In this approach, we will iterate through all the factors of the given number and check if each factor is a perfect square or not. If a factor is a perfect square, we will increment the count.

• Define a function count_perfect_squares_factors1 that takes a single parameter N.
• Initialize a variable count to 0 to keep track of the number of perfect square factors.
• Loop through all the numbers from 1 to N using the range function.
• Check if the current number i is a factor of N and a perfect square using the N % i == 0 and math.sqrt(i) == int(math.sqrt(i)) conditions, respectively.
• If i is a perfect square factor, increment count.
• Return the final value of count.
• Print the result of calling count_perfect_squares_factors1 with some example inputs to verify that the function works as expected.

C++

#include <cmath>
#include <iostream>

int count_perfect_squares_factors1(int N)
{
    int count = 0;
    for (int i = 1; i <= N; ++i) {
        if (N % i == 0
            && std::sqrt(i)
                   == static_cast<int>(std::sqrt(i))) {
            count++;
        }
    }
    return count;
}

int main()
{
    // Example usage
    std::cout << count_perfect_squares_factors1(100)
              << std::endl; // Output: 4
    std::cout << count_perfect_squares_factors1(900)
              << std::endl; // Output: 8
    return 0;
}

Java

import java.util.Scanner;

public class Main {

    // Function to count perfect square factors of N
    static int countPerfectSquareFactors(int N)
    {
        int count = 0;
        for (int i = 1; i <= N; ++i) {
            if (N % i == 0
                && Math.sqrt(i) == (int)Math.sqrt(i)) {
                count++;
            }
        }
        return count;
    }

    public static void main(String[] args)
    {
        // Example usage
        System.out.println(
            countPerfectSquareFactors(100)); // Output: 4
        System.out.println(
            countPerfectSquareFactors(900)); // Output: 8
    }
}

Python3

import math

def count_perfect_squares_factors1(N):
    count = 0
    for i in range(1, N+1):
        if N % i == 0 and math.sqrt(i) == int(math.sqrt(i)):
            count += 1
    return count

# example usage
print(count_perfect_squares_factors1(100)) # output: 4
print(count_perfect_squares_factors1(900)) # output: 8

C#

using System;

class Program {
    // Function to count the number of perfect square
    // factors of N
    static int CountPerfectSquareFactors(int N)
    {
        int count = 0;
        for (int i = 1; i <= N; ++i) {
            if (N % i == 0
                && Math.Sqrt(i) == (int)Math.Sqrt(i)) {
                count++;
            }
        }
        return count;
    }

    static void Main()
    {
        // Example usage
        Console.WriteLine(CountPerfectSquareFactors(100));
        // Output: 4

        Console.WriteLine(CountPerfectSquareFactors(900));
        // Output: 8
    }
}

Javascript

// Function to count the number of factors of N that are perfect squares
function countPerfectSquaresFactors(N) {
    let count = 0; // Initialize a count to keep track of perfect square factors
    for (let i = 1; i <= N; i++) { // Loop from 1 to N
        if (N % i === 0 && Math.sqrt(i) === Math.floor(Math.sqrt(i))) {
            // Check if i is a factor of N and if the square root of i is an integer
            // If both conditions are met, it means i is a perfect square factor of N
            count++; // Increment the count
        }
    }
    return count; // Return the total count of perfect square factors
}

// Example usage
console.log(countPerfectSquaresFactors(100)); // Output: 4
console.log(countPerfectSquaresFactors(900)); // Output: 8

Output

4
8

Time complexity: O(N)
Space complexity: O(1)