Pentadecagonal Number

Given a number N, the task is to find the N^th Pentadecagonal number. 

A Pentadecagonal number is a figurate number that extends the concept of triangular and square numbers to the pentadecagon(a 15-sided polygon). The N^th pentadecagonal number counts the number of dots in a pattern of N nested pentadecagons, all sharing a common corner, where the i^th tridecagon in the pattern has sides made of ‘i’ dots spaced one unit apart from each other. The first few Pentadecagonal numbers are 1, 15, 42, 82, 135, 201, 280 …

Examples:

Input: N = 2 
Output: 15 
Explanation:
The second Pentadecagonal number is 15. 
Input: N = 6 
Output: 201 

Approach: The N^th Pentadecagonal number is given by the formula: 

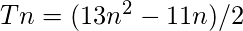
Below is the implementation of the above approach:

C++

// C++ program to find Nth
// Pentadecagonal number
#include <bits/stdc++.h>
using namespace std;

// Function to find N-th
// Pentadecagonal number
int Pentadecagonal_num(int n)
{
    // Formula to calculate nth
    // Pentadecagonal number
    return (13 * n * n - 11 * n) / 2;
}

// Driver code
int main()
{
    int n = 3;
    cout << Pentadecagonal_num(n) << endl;

    n = 10;
    cout << Pentadecagonal_num(n) << endl;

    return 0;
}

Java

// Java program to find Nth
// pentadecagonal number
import java.io.*;
import java.util.*;

class GFG{

// Function to find N-th
// pentadecagonal number
static int Pentadecagonal_num(int n)
{

    // Formula to calculate nth
    // Pentadecagonal number
    return (13 * n * n - 11 * n) / 2;
}

// Driver code
public static void main(String[] args)
{
    int n = 3;
    System.out.println(Pentadecagonal_num(n));

    n = 10;
    System.out.println(Pentadecagonal_num(n));
}
}

// This code is contributed by coder001

Python3

# Python3 program to find Nth
# pentadecagonal number

# Function to find N-th
# pentadecagonal number
def Pentadecagonal_num(n):

    # Formula to calculate nth
    # pentadecagonal number
    return (13 * n * n - 11 * n) / 2

# Driver code
n = 3
print(int(Pentadecagonal_num(n)))

n = 10
print(int(Pentadecagonal_num(n)))

# This code is contributed by divyeshrabadiya07

C#

// C# program to find Nth
// pentadecagonal number
using System;
class GFG{

// Function to find N-th
// pentadecagonal number
static int Pentadecagonal_num(int n)
{

    // Formula to calculate nth
    // Pentadecagonal number
    return (13 * n * n - 11 * n) / 2;
}

// Driver code
public static void Main(string[] args)
{
    int n = 3;
    Console.Write(Pentadecagonal_num(n) + "\n");

    n = 10;
    Console.Write(Pentadecagonal_num(n) + "\n");
}
}

// This code is contributed by rutvik_56

Javascript

<script>

    // Javascript program to find Nth
    // Pentadecagonal number

    // Function to find N-th
    // Pentadecagonal number
    function Pentadecagonal_num(n)
    {
        // Formula to calculate nth
        // Pentadecagonal number
        return (13 * n * n - 11 * n) / 2;
    }

    let n = 3;
    document.write(Pentadecagonal_num(n) + "</br>");

    n = 10;
    document.write(Pentadecagonal_num(n));

</script>

Output:

42
595

Time complexity: O(1) as it is doing constant operations

Auxiliary space: O(1) as it is using constant space for variables

Reference: https://en.wikipedia.org/wiki/Polygonal_number