Pell Number

Pell numbers are numbers that are similar to the Fibonacci numbers and are generated by the below formula as follows: 

Pn = 2*Pn-1 + Pn-2 
with seeds P0 = 0 and P1 = 1

First few Pell numbers are 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461, …. Write a function int pell(int n) that returns P_n.

Examples:

Input : n = 4
Output :12

Input  : n = 7
Output : 169

Method 1 (Using Recursion)

C++

// Pell Number Series using Recursion in C++

#include <bits/stdc++.h>

using namespace std;

// calculate nth pell number
int pell(int n)
{
    if (n <= 2)
        return n;
    return 2 * pell(n - 1) + pell(n - 2);
}

// Driver Code
int main()
{
    int n = 4;
    cout << " " << pell(n);
    return 0;
}

// This code is contributed by shivanisinghss2110

C

// Pell Number Series using Recursion in C
#include <stdio.h>

// calculate nth pell number
int pell(int n)
{
    if (n <= 2)
        return n;
    return 2 * pell(n - 1) + pell(n - 2);
}

// driver function
int main()
{
    int n = 4;
    printf("%d", pell(n));
    return 0;
}

Java

// Pell Number Series using Recursion in JAVA
class PellNumber {

    // calculate n-th Pell number
    public static int pell(int n)
    {
        if (n <= 2)
            return n;
        return 2 * pell(n - 1) + pell(n - 2);
    }

    // driver function
    public static void main(String args[])
    {
        int n = 4;
        System.out.println(pell(n));
    }
}

Python3

# Pell Number Series using
# Recursion in Python3

# Calculate nth pell number
def pell(n) :
    if (n <= 2) :
        return n
    return (2 * pell(n - 1) + pell(n - 2))

# Driver function
n = 4;
print(pell(n))

# This code is contributed by Nikita Tiwari.

C#

// Pell Number Series using Recursion in C#
using System;

class PellNumber {

    // calculate n-th Pell number
    public static int pell(int n)
    {
        if (n <= 2)
            return n;
        return 2 * pell(n - 1) + pell(n - 2);
    }

    // Driver function
    public static void Main()
    {
        int n = 4;
        Console.Write(pell(n));
    }
}

// This code is contributed by vt_m.

PHP

<?php
// Pell Number Series using
// Recursion in PHP

// calculate nth pell number
function pell($n)
{
    if ($n <= 2)
        return $n;
    return 2 * pell($n - 1) +
               pell($n - 2);
}

// Driver Code
$n = 4;
echo(pell($n));

// This code is contributed by Ajit.
?>

Javascript

<script>
// Pell Number Series using
// Recursion in Javascript

// calculate nth pell number
function pell(n)
{
    if (n <= 2)
        return n;
    return 2 * pell(n - 1) +
            pell(n - 2);
}

// Driver Code
let n = 4;
document.write(pell(n));

// This code is contributed by _saurabh_jaiswal.
</script>

Output

 12

Time Complexity: O(2ⁿ) i.e exponential time complexity.

Auxiliary Space: O(n)

Method 2 (Iterative)

C++

// Iterative Pell Number Series in C++
#include <bits/stdc++.h>
using namespace std;

// Calculate nth pell number
int pell(int n)
{
    if (n <= 2)
        return n;

    int a = 1;
    int b = 2;
    int c, i;
    for (i = 3; i <= n; i++) {
        c = 2 * b + a;
        a = b;
        b = c;
    }
    return b;
}

// Driver Code
int main()
{
    int n = 4;

    cout << pell(n);
    return 0;
}

// This code is contributed by nidhi_biet

C

// Iterative Pell Number Series in C
#include <stdio.h>

// calculate nth pell number
int pell(int n)
{
    if (n <= 2)
        return n;

    int a = 1;
    int b = 2;
    int c, i;
    for (i = 3; i <= n; i++) {
        c = 2 * b + a;
        a = b;
        b = c;
    }
    return b;
}

// driver function
int main()
{
    int n = 4;
    printf("%d", pell(n));
    return 0;
}

Java

// Iterative Pell Number Series in Java
class PellNumber {

    // calculate nth pell number
    public static int pell(int n)
    {
        if (n <= 2)
            return n;
        int a = 1;
        int b = 2;
        int c;
        for (int i = 3; i <= n; i++) {
            c = 2 * b + a;
            a = b;
            b = c;
        }
        return b;
    }

    // driver function
    public static void main(String args[])
    {
        int n = 4;
        System.out.println(pell(n));
    }
}

Python

# Iterative Pell Number
# Series in Python 3

# calculate nth pell number
def pell(n) :
    if (n <= 2) :
        return n

    a = 1
    b = 2
    for i in range(3, n+1) :
        c = 2 * b + a
        a = b
        b = c

    return b

# driver function
n = 4
print(pell(n))

# This code is contributed by Nikita Tiwari.

C#

// Iterative Pell Number Series in C#
using System;
class PellNumber {

    // calculate nth pell number
    public static int pell(int n)
    {
        if (n <= 2)
            return n;
        int a = 1;
        int b = 2;
        int c;
        for (int i = 3; i <= n; i++) {
            c = 2 * b + a;
            a = b;
            b = c;
        }
        return b;
    }

    // Driver function
    public static void Main()
    {
        int n = 4;
        Console.Write(pell(n));
    }
}

// This code is contributed by vt_m.

PHP

<?php
// Iterative Pell Number Series in PHP

// calculate nth pell number
function pell($n)
{
    if ($n <= 2)
        return $n;

    $a = 1;
    $b = 2;
    $c; $i;
    for ($i = 3; $i <= $n; $i++)
    {
        $c = 2 * $b + $a;
        $a = $b;
        $b = $c;
    }
    return $b;
}

// Driver Code
$n = 4;
echo(pell($n));

// This code is contributed by Ajit.
?>

Javascript

<script>
    // Iterative Pell Number Series in Javascript

    // calculate nth pell number
    function pell(n)
    {
        if (n <= 2)
            return n;
        let a = 1;
        let b = 2;
        let c;
        for (let i = 3; i <= n; i++) {
            c = 2 * b + a;
            a = b;
            b = c;
        }
        return b;
    }

    let n = 4;
      document.write(pell(n));

</script>

Output:

12

Time Complexity: O(n) 

Auxiliary Space: O(1)

Using matrix calculation: 

This another O(n) that relies on the fact that if we n times multiply the matrix M = {{2, 1}, {1, 0}} to itself (in other words calculate power(M, n)), then we get the (n+1)th Pell number as the element at row and column (0, 0) in the resultant matrix.

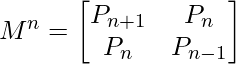
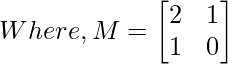
Time Complexity: O(log n) Since we can compute n-th power of a 2 × 2 matrix in O(log n) times