Parzen Windows density estimation technique
Last Updated :
04 Jan, 2022
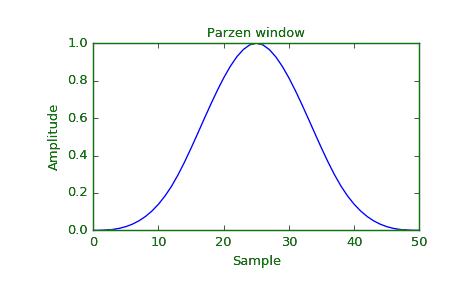
Parzen Window is a non-parametric density estimation technique. Density estimation in Pattern Recognition can be achieved by using the approach of the Parzen Windows. Parzen window density estimation technique is a kind of generalization of the histogram technique.
It is used to derive a density function, 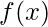 .
.
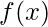 is used to implement a Bayes Classifier. When we have a new sample feature
is used to implement a Bayes Classifier. When we have a new sample feature 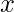 and when there is a need to compute the value of the class conditional densities,
and when there is a need to compute the value of the class conditional densities, 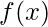 is used.
is used.
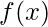 takes sample input data value and returns the density estimate of the given data sample.
takes sample input data value and returns the density estimate of the given data sample.
An n-dimensional hypercube is considered which is assumed to possess k-data samples.
The length of the edge of the hypercube is assumed to be hn.
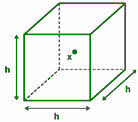
Hence the volume of the hypercube is: Vn = hnd
We define a hypercube window function, φ(u) which is an indicator function of the unit hypercube which is centered at origin.:
φ(u) = 1 if |ui| <= 0.5
φ(u) = 0 otherwise
Here, u is a vector, u = (u1, u2, …, ud)T.
φ(u) should satisfy the following:
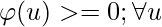
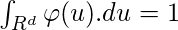
Let 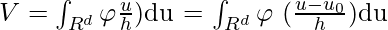
Since, φ(u) is centered at the origin, it is symmetric.
φ(u) = φ(-u)
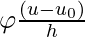 is a hypercube of size h centered at u0
is a hypercube of size h centered at u0- Let D = {x1, x2, …, xn} be the data samples.
- For any
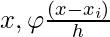 would be 1 only if
would be 1 only if 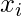 falls in a hypercube of side
falls in a hypercube of side 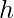 centered at
centered at 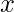 .
. - Hence the number of data points falling in a hypercube of side h centered at x is
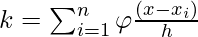
Hence the estimated density function is :
*** QuickLaTeX cannot compile formula:
*** Error message:
Error: Nothing to show, formula is empty
Also Since,
Vn = hnd, Density Function becomes :
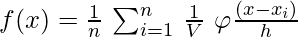
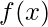
would satisfy the following conditions:
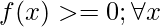
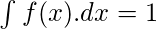
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...