Parsing and Syntax directed translation

Question 1

What is the maximum number of reduce moves that can be taken by a bottom-up parser for a grammar with no epsilon- and unit-production (i.e., of type A -> є and A -> a) to parse a string with n tokens?

• n/2

• n-1

• 2n-1

• 2ⁿ

Question 2

Consider the following two sets of LR(1) items of an LR(1) grammar.

X -> c.X, c/d
   X -> .cX, c/d
   X -> .d, c/d
   X -> c.X, $
   X -> .cX, $
   X -> .d, $

Which of the following statements related to merging of the two sets in the corresponding LALR parser is/are FALSE?

1. Cannot be merged since look aheads are different.
2. Can be merged but will result in S-R conflict.
3. Can be merged but will result in R-R conflict.
4. Cannot be merged since goto on c will lead to two different sets.

• 1 only
• 2 only
• 1 and 4 only
• 1, 2, 3, and 4

Question 3

For the grammar below, a partial LL(1) parsing table is also presented along with the grammar. Entries that need to be filled are indicated as E1, E2, and E3. [Tex]\\epsilon[/Tex] is the empty string, $ indicates end of input, and, | separates alternate right hand sides of productions.

• A
• B
• C
• D

Question 4

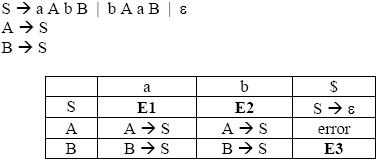
Consider the date same as above question. The appropriate entries for E1, E2, and E3 are 

[caption width="800"]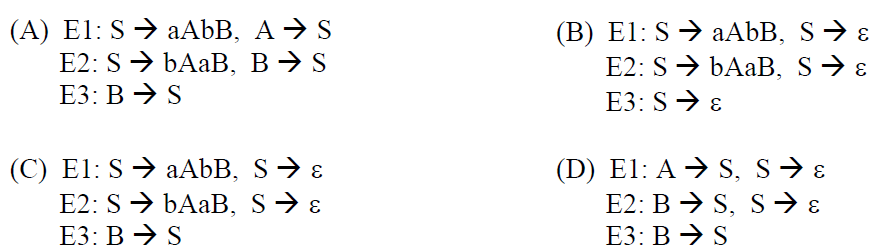 [/caption]

• A

• B

• C

• D

Question 5

The grammar S → aSa | bS | c is

• LL(1) but not LR(1)

• LR(1)but not LR(1)

• Both LL(1)and LR(1)

• Neither LL(1)nor LR(1)

Question 6

Match all items in Group 1 with correct options from those given in Group 2.

Group 1                          Group 2
P. Regular expression        1. Syntax analysis
Q. Pushdown automata         2. Code generation
R. Dataflow analysis         3. Lexical analysis
S. Register allocation       4. Code optimization

• P-4. Q-1, R-2, S-3
• P-3, Q-1, R-4, S-2
• P-3, Q-4, R-1, S-2
• P-2, Q-1, R-4, S-3

Question 7

Which of the following statements are TRUE?

I.  There exist parsing algorithms for some programming languages 
     whose complexities are less than O(n3).
II.  A programming language which allows recursion can be implemented 
    with static storage allocation.
III. No L-attributed definition can be evaluated in The framework 
     of bottom-up parsing.
IV. Code improving transformations can be performed at both source 
    language and intermediate code level.

• I and II
• I and IV
• III and IV
• I, III and IV

Question 8

Which of the following describes a handle (as applicable to LR-parsing) appropriately?

• It is the position in a sentential form where the next shift or reduce operation will occur
• It is non-terminal whose production will be used for reduction in the next step
• It is a production that may be used for reduction in a future step along with a position in the sentential form where the next shift or reduce operation will occur
• It is the production p that will be used for reduction in the next step along with a position in the sentential form where the right hand side of the production may be found

Question 9

An LALR(1) parser for a grammar G can have shift-reduce (S-R) conflicts if and only if

• the SLR(1) parser for G has S-R conflicts
• the LR(1) parser for G has S-R conflicts
• the LR(0) parser for G has S-R conflicts
• the LALR(1) parser for G has reduce-reduce conflicts

Question 10

Which one of the following is a top-down parser?

• Recursive descent parser.
• Operator precedence parser.
• An LR(k) parser.
• An LALR(k) parser