Parity of the given mathematical expression using given N numbers
Last Updated :
31 Jan, 2023
Given N positive integers A1, A2, …, AN, the task is to determine the parity of the expression S.
For the given N numbers, the expression S is given as:
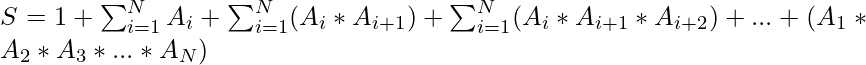
Examples:
Input: N = 3, A1 = 2, A2 = 3, A3 = 1
Output: Even
Explanation:
S = 1 + (2 + 3 + 1) + (2*3 + 3*1 + 1*2) + (2*3*1) = 24, which is even
Input: N = 2, A1 = 2, A2 = 4
Output: Odd
Explanation:
S = 1 + (2 + 4) + (2 * 4) = 15, which is odd
Naive Approach: The naive approach for this problem is to plug in all the values of Ai in the given expression and find the parity of the given expression. This method doesn’t work for higher values of N as the multiplication is not a constant operation for higher-ordered numbers. And also, the value might become so large that it might cause integer overflow.
Efficient Approach: The idea is to perform some processing on the expression and reduce the expression into simpler terms so that the parity can be checked without computing the value. Let N = 3. Then:
1 + (A1 + A2 + A3) + ((A1 * A2) + (A2 * A3) + (A3 * A1) + (A1 * A2 * A3)
- Now, the same expression is restructured as follows:
(1 + A1) + (A2 + A1 * A2) + (A3 + A3 * A1) + (A2 * A3 + A1 * A2 * A3)
=> (1 + A1) + A2 * (1 + A1) + A3 * (1 + A1) + A2 * A3 * (1 + A1)
- On taking (1 + A1) common from the above equation,
(1 + A1) * (1 + A2 + A2 + (A2 * A3))
=> (1 + A1) * (1 + A2 + A3 * (1 + A2)
- Finally, on taking (1 + A2) common, the final expression becomes:
(1 + A1) * (1 + A2) * (1 + A3)
- By symmetry, for N elements, the expression S becomes:
(1 + A1) * (1 + A2) * (1 + A3) … * (1 + AN)
- Clearly, for a number to become even parity, the answer must be even. It is known that the answer is even if any of the numbers are even.
- Therefore, the idea is to check if any of the numbers in the given input is odd. If it is, then on adding one, it becomes even and the value is even parity.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void getParity(
int n,
const vector<int>& A)
{
for (auto x : A) {
if (x & 1) {
cout << "Even" << endl;
return;
}
}
cout << "Odd" << endl;
}
int main()
{
int N = 3;
vector<int> A = { 2, 3, 1 };
getParity(N, A);
return 0;
}
|
Java
class GFG{
static void getParity(int n, int []A)
{
for (int x : A)
{
if ((x & 1) == 1)
{
System.out.println("Even");
return;
}
}
System.out.println("Odd");
}
public static void main(String[] args)
{
int N = 3;
int [] A = { 2, 3, 1 };
getParity(N, A);
}
}
|
Python3
def getParity(n, A):
for x in A:
if (x & 1):
print("Even")
return
print("Odd")
if __name__ == '__main__':
N = 3
A = [ 2, 3, 1 ]
getParity(N, A)
|
C#
using System;
public class GFG{
static void getParity(int n, int []A)
{
foreach (int x in A)
{
if ((x & 1) == 1)
{
Console.WriteLine("Even");
return;
}
}
Console.WriteLine("Odd");
}
public static void Main(string[] args)
{
int N = 3;
int [] A = { 2, 3, 1 };
getParity(N, A);
}
}
|
Javascript
<script>
function getParity(n, A)
{
for (let x in A)
{
if ((x & 1) == 1)
{
document.write("Even");
return;
}
}
document.write("Odd");
}
let N = 3;
let A = [ 2, 3, 1 ];
getParity(N, A);
</script>
|
Time Complexity: O(N), where N is the number of given numbers.
Space Complexity : O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...