Pair of integers having difference of their fifth power as X
Last Updated :
07 Apr, 2021
Given an integer X, the task is to find a pair A and B such that their difference of fifth power is X, i.e., A5 – B5 = X. If there is no such pair print “Not Possible”.
Input: X = 33
Output: 1 -2
Explanation:
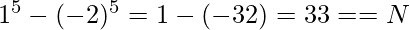
Input: N = 211
Output: -2 -3
Explanation:
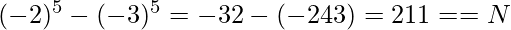
Naive Approach: A simple solution is to use two for loops, one for A and one for B, ranging from -109 to 109.
Efficient Approach: The idea is to narrow down the range of A and B using mathematical techniques.
Since A5 – B5 = X => A5 = X + B5. For A to be as high as possible, B also has to be as high as possible, as it is evident from the inequality.
Consider A = N and B = N – 1
=> N5 – (N – 1)5 = X.
By binomial expansion, we know
(p + 1)yp <= (y + 1)p+1 – yp+1 <= (p+1)(y+1)p
So we can say that the maximum value of LHS is 4N4.
Hence 4N5 <= X
=> N <= (X/5)1/5.
=> This gives us N ~ 120.
Since A and B can also be negative, we simply extrapolate the range and the final range we get is [-120, 120].
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findPair(int x)
{
int lim = 120;
for (int i = -lim; i <= lim; i++) {
for (int j = -lim; j <= lim; j++) {
if (pow(i, 5) - pow(j, 5) == x) {
cout << i << ' ' << j << endl;
return;
}
}
}
cout << "-1";
}
signed main()
{
int X = 33;
findPair(X);
return 0;
}
|
Java
class GFG{
static void findPair(int x)
{
int lim = 120;
for(int i = -lim; i <= lim; i++)
{
for(int j = -lim; j <= lim; j++)
{
if (Math.pow(i, 5) -
Math.pow(j, 5) == x)
{
System.out.print(i + " " +
j + "\n");
return;
}
}
}
System.out.print("-1");
}
public static void main(String[] args)
{
int X = 33;
findPair(X);
}
}
|
Python3
import math
def findPair(x):
lim = 120
for i in range(-lim, lim + 1):
for j in range(-lim, lim + 1):
if (math.pow(i, 5) -
math.pow(j, 5) == x):
print (i, end = ' ')
print (j, end = '\n')
return
print ("-1")
X = 33
findPair(X)
|
C#
using System;
class GFG{
static void findPair(int x)
{
int lim = 120;
for(int i = -lim; i <= lim; i++)
{
for(int j = -lim; j <= lim; j++)
{
if (Math.Pow(i, 5) -
Math.Pow(j, 5) == x)
{
Console.Write(i + " " +
j + "\n");
return;
}
}
}
Console.Write("-1");
}
public static void Main(String[] args)
{
int X = 33;
findPair(X);
}
}
|
Javascript
<script>
function findPair(x)
{
let lim = 120;
for(let i = -lim; i <= lim; i++)
for(let j = -lim; j <= lim; j++)
if (Math.pow(i, 5) -Math.pow(j, 5) == x)
{
document.write(i + " "+ j);
return;
}
document.write("-1");
}
let X = 33;
findPair(X);
</script>
|
Time Complexity: O(240*240)
Share your thoughts in the comments
Please Login to comment...