Overlapping Subproblems Property in Dynamic Programming | DP-1
Last Updated :
08 Mar, 2023
Dynamic Programming is an algorithmic paradigm that solves a given complex problem by breaking it into subproblems using recursion and storing the results of subproblems to avoid computing the same results again. Following are the two main properties of a problem that suggests that the given problem can be solved using Dynamic programming.
- Overlapping Subproblems
- Optimal Substructure
In this post, we will discuss the first property Overlapping Subproblems in detail. The second property of Dynamic programming is discussed in the next post.
Overlapping Subproblems:
Like Divide and Conquer, Dynamic Programming combines solutions to sub-problems. Dynamic Programming is mainly used when solutions to the same subproblems are needed again and again. In dynamic programming, computed solutions to subproblems are stored in a table so that these don’t have to be recomputed. So Dynamic Programming is not useful when there are no common (overlapping) subproblems because there is no point in storing the solutions if they are not needed again. For example, Binary Search doesn’t have common subproblems. If we take the example of following a recursive program for Fibonacci Numbers, there are many subproblems that are solved again and again.
C++
#include <iostream>
using namespace std;
int fib(int n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
int main() {
cout << fib(7);
return 0;
}
|
C
int fib(int n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
|
Java
static int fib(int n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
|
Python
def fib(n):
if n <= 1:
return n
return fib(n - 1) + fib(n - 2)
|
C#
static int fib(int n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
|
Javascript
<script>
function fib(n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
</script>
|
Time Complexity: O(2N)
Auxiliary Space: O(1)
Illustration of Recursion tree for the execution of fib(5) :
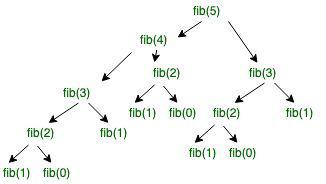
Recursion tree for the execution of fib(5)
We can see that the function fib(3) is being called 2 times. If we would have stored the value of fib(3), then instead of computing it again, we could have reused the old stored value. There are following two different ways to store the values so that these values can be reused:
- Memoization (Top Down)
- Tabulation (Bottom Up)
Memoization (Top Down):
The memoized program for a problem is similar to the recursive version with a small modification that looks into a lookup table before computing solutions. We initialize a lookup array with all initial values as NIL. Whenever we need the solution to a subproblem, we first look into the lookup table. If the precomputed value is there then we return that value, otherwise, we calculate the value and put the result in the lookup table so that it can be reused later.
Following is the memoized version for the nth Fibonacci Number.
C++
#include <bits/stdc++.h>
using namespace std;
#define NIL -1
#define MAX 100
int lookup[MAX];
void _initialize()
{
int i;
for (i = 0; i < MAX; i++)
lookup[i] = NIL;
}
int fib(int n)
{
if (lookup[n] == NIL) {
if (n <= 1)
lookup[n] = n;
else
lookup[n] = fib(n - 1) + fib(n - 2);
}
return lookup[n];
}
int main()
{
int n = 40;
_initialize();
cout << "Fibonacci number is " << fib(n);
return 0;
}
|
C
#include <stdio.h>
#define NIL -1
#define MAX 100
int lookup[MAX];
void _initialize()
{
int i;
for (i = 0; i < MAX; i++)
lookup[i] = NIL;
}
int fib(int n)
{
if (lookup[n] == NIL) {
if (n <= 1)
lookup[n] = n;
else
lookup[n] = fib(n - 1) + fib(n - 2);
}
return lookup[n];
}
int main()
{
int n = 40;
_initialize();
printf("Fibonacci number is %d ", fib(n));
return 0;
}
|
Java
public class Fibonacci {
final int MAX = 100;
final int NIL = -1;
int lookup[] = new int[MAX];
void _initialize()
{
for (int i = 0; i < MAX; i++)
lookup[i] = NIL;
}
int fib(int n)
{
if (lookup[n] == NIL) {
if (n <= 1)
lookup[n] = n;
else
lookup[n] = fib(n - 1) + fib(n - 2);
}
return lookup[n];
}
public static void main(String[] args)
{
Fibonacci f = new Fibonacci();
int n = 40;
f._initialize();
System.out.println("Fibonacci number is"
+ " " + f.fib(n));
}
}
|
Python
def fib(n, lookup):
if n <= 1:
lookup[n] = n
if lookup[n] is None:
lookup[n] = fib(n-1, lookup) + fib(n-2, lookup)
return lookup[n]
def main():
n = 34
lookup = [None] * 101
print "Fibonacci Number is ", fib(n, lookup)
if __name__ == "__main__":
main()
|
C#
using System;
class GFG {
static int MAX = 100;
static int NIL = -1;
static int[] lookup = new int[MAX];
static void initialize()
{
for (int i = 0; i < MAX; i++)
lookup[i] = NIL;
}
static int fib(int n)
{
if (lookup[n] == NIL) {
if (n <= 1)
lookup[n] = n;
else
lookup[n] = fib(n - 1) + fib(n - 2);
}
return lookup[n];
}
public static void Main()
{
int n = 40;
initialize();
Console.Write("Fibonacci number is"
+ " " + fib(n));
}
}
|
Javascript
<script>
let MAX = 100;
let NIL = -1;
let lookup = new Array(MAX);
function _initialize()
{
for (let i = 0; i < MAX; i++)
lookup[i] = NIL;
}
function fib(n)
{
if (lookup[n] == NIL)
{
if (n <= 1)
lookup[n] = n;
else
lookup[n] = fib(n-1) + fib(n-2);
}
return lookup[n];
}
let n = 40;
_initialize();
document.write("Fibonacci number is" + " " + fib(n)+"<br>");
</script>
|
Output
Fibonacci number is 102334155
Time Complexity: O(N). This is because the algorithm computes each Fibonacci number only once and stores the result in an array for future use. Subsequent calls to the function with the same input value of n will retrieve the stored value from the lookup table, avoiding the need to recompute it. Therefore, the time complexity is linear, and the algorithm is very efficient for large values of n.
Space Complexity: O(N) as lookup table has been created.
Tabulation (Bottom Up):
The tabulated program for a given problem builds a table in a bottom-up fashion and returns the last entry from the table. For example, for the same Fibonacci number, we first calculate fib(0) then fib(1) then fib(2) then fib(3), and so on. So literally, we are building the solutions to subproblems bottom-up.
Following is the tabulated version for the nth Fibonacci Number.
C
#include <stdio.h>
int fib(int n)
{
int f[n + 1];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
f[i] = f[i - 1] + f[i - 2];
return f[n];
}
int main()
{
int n = 9;
printf("Fibonacci number is %d ", fib(n));
return 0;
}
|
Java
public class Fibonacci {
int fib(int n)
{
int f[] = new int[n + 1];
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= n; i++)
f[i] = f[i - 1] + f[i - 2];
return f[n];
}
public static void main(String[] args)
{
Fibonacci f = new Fibonacci();
int n = 9;
System.out.println("Fibonacci number is"
+ " " + f.fib(n));
}
}
|
Python
def fib(n):
f = [0] * (n + 1)
f[1] = 1
for i in xrange(2, n + 1):
f[i] = f[i - 1] + f[i - 2]
return f[n]
def main():
n = 9
print "Fibonacci number is ", fib(n)
if __name__ == "__main__":
main()
|
C#
using System;
class GFG {
static int fib(int n)
{
int[] f = new int[n + 1];
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= n; i++)
f[i] = f[i - 1] + f[i - 2];
return f[n];
}
public static void Main()
{
int n = 9;
Console.Write("Fibonacci number is"
+ " " + fib(n));
}
}
|
Javascript
<script>
function fib(n)
{
var f = new Array(n + 1);
var i;
f[0] = 0;
f[1] = 1;
for(i = 2; i <= n; i++)
f[i] = f[i - 1] + f[i - 2];
return f[n];
}
var n = 9;
document.write("Fibonacci number is " + fib(n));
</script>
|
PHP
<?php
function fib($n)
{
$f[$n + 1]=0;
$i;
$f[0] = 0;
$f[1] = 1;
for ($i = 2; $i <= $n; $i++)
$f[$i] = $f[$i - 1] +
$f[$i - 2];
return $f[$n];
}
$n = 9;
echo("Fibonacci number is ");
echo(fib($n));
?>
|
C++
#include <iostream>
using namespace std;
int fib(int n)
{
int f[n + 1];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
f[i] = f[i - 1] + f[i - 2];
return f[n];
}
int main()
{
int n = 9;
printf("Fibonacci number is %d ", fib(n));
return 0;
}
|
Output
Fibonacci number is 34
Time Complexity: O(N)
Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...