Optimum Global Thresholding Using Otsu’s Method

Last Updated : 09 Mar, 2023

Image thresholding is one of the segmentation techniques, that segments or divided the image into two or more different parts based on pixel intensities. There are many different algorithms for carrying out thresholding and here we are going to see one of the most efficient and optimum techniques called Otsu’s method.

What is Image Thresholding?

Thresholding is the technique of generating a binary image (a binary image is one whose pixels have only two values – 0 and 1 and thus require only one bit to store pixel intensity) from a given greyscale image by separating it into two regions based on a threshold value. Hence pixels having intensity values greater than the said threshold will be treated as white or 1 in the output image and the others will be black or 0.

In other words, if we have a threshold T, then the segmented image g(x,y) is computed as shown below:

g(x,y) = 1 if f(x,y) > T 
and g(x,y) = 0 if f(x,y) ≤ T.

So the output segmented image has only two classes of pixels – one having a value of 1 and others having a value of 0.

Otsu’s Thresholding Method

Otsu’s method is a technique of performing global thresholding on a digital image. It is optimum in the sense that it maximizes the between-class variance. The basic crux of the method is that well-thresholded classes of pixels must be distinct with respect to the intensity levels of their pixels and conversely, a threshold that gives the best separation between two different classes of pixels in terms of their intensity levels would be the optimum or the best threshold.

1. Let {0, 1, 2, 3,… , L-1} denote the L distinct intensity levels of the pixels in an M x N image.

2. Let ni denote the number of pixels with intensity level i. Total number of pixels in the image M_N = n_o + n_1 + …. + n_{L-1}.

3. The normalized histogram of the image will have components as probabilities of occurrence of an intensity level i as: 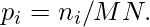$p_i = n_i/MN.$

4. Clearly, we must have:

$\sum_{i=0}^{L-1}p_{i}=1$

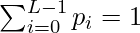
5. Let us pick a threshold T = k, where 0 < k < L-1. Using this threshold T, we segment the image into two separate classes C1 and C2.

C1 consists of all pixels with intensity values in the range [0, k].
C2 consists of pixels with intensity values in the range [k+1, L-1].

6. The probability that a pixel belongs to the class C1 P1(k) is given by:

$P_{1}(k) = \sum_{i=0}^{k}p_{i}$

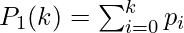
If we have k = 0, the probability of class C1 having any pixel is basically zero.

7. Similarly, the probability of class C2 is:

$P_{2}(k) = 1- P_{1}(k) = 1 - \sum_{i=0}^{k}p_{i} = \sum_{i=k+1}^{L-1}p_{i}$

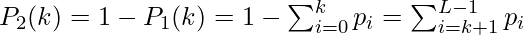
8. Now, the mean intensity level of the pixels belonging to class C1 is:

$m_{1}(k) = \sum_{i=0}^{k}iP(i|C_{1}) = \sum_{i=0}^{k}i\frac{P(C_{1}|i)P(i)}{P(C_{1})} = \frac{1}{P_{1}(k)}\sum_{i=0}^{k}ip_{i}$

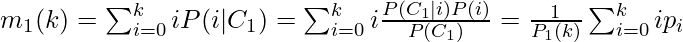
Here, P(i|C1) is the probability of occurrence of intensity value i given that it is class C1.

9. Using Baye’s theorem in the above simplification we get:

$P(i|C_{1}) = \frac{P(C_{1}|i)P(i)}{P(C_{1})}$

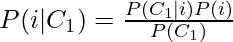
Here, P(C1|i) is the probability of class C1 given that it is of intensity level i. This is obviously 1, as we are dealing with intensity values from class C1 only.

P(i) is the probability of the ith intensity value which is pi
P(C1) is the probability of class C1, which is, as computed above, equal to P1(k).

10. Similarity, by carrying over the same arguments for class C2, the mean intensity level of pixels of class C2 is:

$m_{2}(k)=\sum_{i=k+1}^{L-1}iP(i|C_{2})=\frac{1}{P_{2}(k)}\sum_{i=k+1}^{L-1}ip_{i}$

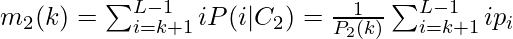
11. The cumulative mean, that is, the average intensity, upto level k is defined as: 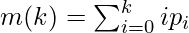$m(k)=\sum_{i=0}^{k}ip_{i}$

12. The average intensity (global mean) of the entire image is just summing over all the levels from 0 to L-1, that is: 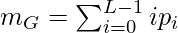$m_G=\sum_{i=0}^{L-1}ip_{i}$

13. From these definitions, we can easily see that: 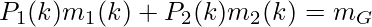$P_{1}(k)m_{1}(k)+P_{2}(k)m_{2}(k) = m_{G}$ and $P_{1}(k)+P_{2}(k)=1$

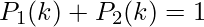
14. Now, we have the global variance as 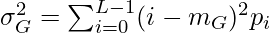$\sigma _{G}^{2}=\sum_{i=0}^{L-1}(i-m_{G})^2p_{i}$ and the between-class variance is defined as:

$\sigma _{B}^{2}(k)=P_{1}(k)[m_{1}(k)-m_{G}]^2+P_{2}(k)[m_{2}(k)-m_{G}]^2$

15. This can also be written as: $\sigma _{B}^{2}(k)=P_{1}(k)P_{2}(k)[m_{1}(k)-m_2(k)]^2 = \frac{[m_GP_{1}(k)-m(k)]^2}{P_{1}(k)[1-P_{1}(k)]}$

16. Next, we define a figure of merit: 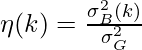$\eta (k)=\frac{\sigma _{B}^{2}(k)}{\sigma _{G}^{2}}$

17. According to Otsu, the optimum threshold k=k’ is the one that maximizes 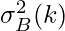$\sigma _{B}^{2}(k)$

$\sigma _{B}^{2}(k')= \underset{0\leq k\leq L-1}{max}[\sigma _{B}^{2}(k)]$

18. If the maximum exists for more than one value of k, then it is customary to take the average of the different maxima values, and assign it to k’. Once we have k’, we can directly segment the image f(x,y) as follows: g(x,y) = 1 if f(x,y)>k’ and g(x,y) = 0 if f(x,y)≤k’

Otsu’s Method Algorithm

Compute the normalized histogram of the input image. Denote the components of the histogram by pi.
Compute the cumulative sums P1(k).
Compute the cumulative mean m(k).
Compute the global intensity mean m_G.
Compute the between-class variance σ_B²(k).
Obtain the optimum threshold k’ for which between-class variance is maximum by iterating over values of k. If more than one maximum exists, obtain k’ by averaging over these values.
Segment the image using the threshold k’ as g(x,y) = 1 if f(x,y)>k’ and g(x,y) = 0 if f(x,y)≤k’.

Implementation

Below is the Matlab code to implement the above approach:

Matlab

% Matlab program to perform Otsu's thresholding 
image=(imread("GFG.jpg")); 
figure(1); 
imshow(image); 
image1=rgb2gray(image); 
[counts,x] = imhist(image1,16); 
thresh= otsuthresh(counts); 
otsu=imbinarize(image1,thresh); 
figure(2); 
imshow(otsu);