Optimal Storage on Tapes
Last Updated :
25 Apr, 2023
Given 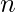 programs stored on a computer tape and length of each program
programs stored on a computer tape and length of each program 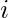 is
is 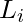 where
where 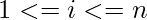 , find the order in which the programs should be stored in the tape for which the Mean Retrieval Time (MRT given as
, find the order in which the programs should be stored in the tape for which the Mean Retrieval Time (MRT given as 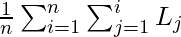 ) is minimized.
) is minimized.
The greedy algorithm finds the MRT as following:
Algorithm MRT_SINGLE_TAPE(L)
// Description: Find storage order of n programs to such that mean retrieval time is minimum
//Input: L is array of program length sorted in ascending order
// Output: Minimum Mean Retrieval Time
Tj <— 0
for i <— 1 to n do
for j <- 1 to i do
Tj <- Tj + L[j]
end
end
MRT <- sum(T) / nComplexity analysis:
Primitive operation in the above algorithm is the addition of program length, which is enclosed within two loops. The running time of algorithm is given by,
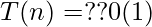
=? ? ?
=?i=1+2+3+…+n
=n(n+1)/2
= n^2/2 + n/2
T(n) =0(n²)
This algorithm runs in O (n²)time.
Example:
Input : n = 3
L[] = { 5, 3, 10 }
Output : Order should be { 3, 5, 10 } with MRT = 29/3
Prerequisites: Magnetic Tapes Data Storage
Let us first break down the problem and understand what needs to be done.
A magnetic tape provides only sequential access of data. In an audio tape/cassette, unlike a CD, a fifth song from the tape can’t be just directly played. The length of the first four songs must be traversed to play the fifth song. So in order to access certain data, head of the tape should be positioned accordingly.
Now suppose there are 4 songs in a tape of audio lengths 5, 7, 3 and 2 mins respectively. In order to play the fourth song, we need to traverse an audio length of 5 + 7 + 3 = 15 mins and then position the tape head.
Retrieval time of the data is the time taken to retrieve/access that data in its entirety. Hence retrieval time of the fourth song is 15 + 2 = 17 mins.
Now, considering that all programs in a magnetic tape are retrieved equally often and the tape head points to the front of the tape every time, a new term can be defined called the Mean Retrieval Time (MRT).
Let’s suppose that the retrieval time of program 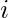 is
is 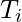 . Therefore,
. Therefore, 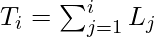
MRT is the average of all such 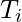 . Therefore
. Therefore 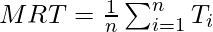 , or
, or 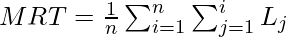
The sequential access of data in a tape has some limitations. Order must be defined in which the data/programs in a tape are stored so that least MRT can be obtained. Hence the order of storing becomes very important to reduce the data retrieval/access time.
Thus, the task gets reduced – to define the correct order and hence minimize the MRT, i.e. to minimize the term 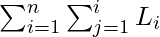
For e.g. Suppose there are 3 programs of lengths 2, 5 and 4 respectively. So there are total 3! = 6 possible orders of storage.
| | Order | Total Retrieval Time | Mean Retrieval Time |
|---|
| 1 | 1 2 3 | 2 + (2 + 5) + (2 + 5 + 4) = 20 | 20/3 |
|---|
| 2 | 1 3 2 | 2 + (2 + 4) + (2 + 4 + 5) = 19 | 19/3 |
|---|
| 3 | 2 1 3 | 5 + (5 + 2) + (5 + 2 + 4) = 23 | 23/3 |
|---|
| 4 | 2 3 1 | 5 + (5 + 4) + (5 + 4 + 2) = 25 | 25/3 |
|---|
| 5 | 3 1 2 | 4 + (4 + 2) + (4 + 2 + 5) = 21 | 21/3 |
|---|
| 6 | 3 2 1 | 4 + (4 + 5) + (4 + 5 + 2) = 24 | 24/3 |
|---|
It’s clear that by following the second order in storing the programs, the mean retrieval time is least.
In above example, the first program’s length is added ‘n’ times, the second ‘n-1’ times…and so on till the last program is added only once. So, careful analysis suggests that in order to minimize the MRT, programs having greater lengths should be put towards the end so that the summation is reduced. Or, the lengths of the programs should be sorted in increasing order. That’s the Greedy Algorithm in use – at each step we make the immediate choice of putting the program having the least time first, in order to build up the ultimate optimized solution to the problem piece by piece.
Below is the implementation:
C++
#include <bits/stdc++.h>
using namespace std;
void findOrderMRT(int L[], int n)
{
sort(L, L + n);
cout << "Optimal order in which programs are to be"
"stored is: ";
for (int i = 0; i < n; i++)
cout << L[i] << " ";
cout << endl;
double MRT = 0;
for (int i = 0; i < n; i++) {
int sum = 0;
for (int j = 0; j <= i; j++)
sum += L[j];
MRT += sum;
}
MRT /= n;
cout << "Minimum Retrieval Time of this"
" order is " << MRT;
}
int main()
{
int L[] = { 2, 5, 4 };
int n = sizeof(L) / sizeof(L[0]);
findOrderMRT(L, n);
return 0;
}
|
Java
import java.io.*;
import java .util.*;
class GFG
{
static void findOrderMRT(int []L,
int n)
{
Arrays.sort(L);
System.out.print("Optimal order in which " +
"programs are to be stored is: ");
for (int i = 0; i < n; i++)
System.out.print(L[i] + " ");
System.out.println();
double MRT = 0;
for (int i = 0; i < n; i++)
{
int sum = 0;
for (int j = 0; j <= i; j++)
sum += L[j];
MRT += sum;
}
MRT /= n;
System.out.print( "Minimum Retrieval Time" +
" of this order is " + MRT);
}
public static void main (String[] args)
{
int []L = { 2, 5, 4 };
int n = L.length;
findOrderMRT(L, n);
}
}
|
Python3
def findOrderMRT(L, n):
L.sort()
print("Optimal order in which programs are to be stored is:", end=" ")
for i in range(0, n):
print(L[i], end=" ")
print()
MRT = 0
for i in range(0, n):
sum = 0
for j in range(0, i+1):
sum += L[j]
MRT += sum
MRT /= n
print("Minimum Retrieval Time of this order is", "{0:.5f}".format(MRT))
L = [2, 5, 4]
n = len(L)
findOrderMRT(L, n)
|
C#
using System;
class GFG
{
static void findOrderMRT(int []L,
int n)
{
Array.Sort(L);
Console.Write("Optimal order in " +
"which programs are" +
" to be stored is: ");
for (int i = 0; i < n; i++)
Console.Write(L[i] + " ");
Console.WriteLine();
double MRT = 0;
for (int i = 0; i < n; i++)
{
int sum = 0;
for (int j = 0; j <= i; j++)
sum += L[j];
MRT += sum;
}
MRT /= n;
Console.WriteLine("Minimum Retrieval " +
"Time of this order is " +
MRT);
}
public static void Main ()
{
int []L = { 2, 5, 4 };
int n = L.Length;
findOrderMRT(L, n);
}
}
|
Javascript
<script>
function findOrderMRT(L, n)
{
L.sort();
document.write("Optimal order in which " +
"programs are to be stored is: ");
for (let i = 0; i < n; i++)
document.write(L[i] + " ");
document.write("<br/>");
let MRT = 0;
for (let i = 0; i < n; i++)
{
let sum = 0;
for (let j = 0; j <= i; j++)
sum += L[j];
MRT += sum;
}
MRT /= n;
document.write( "Minimum Retrieval Time" +
" of this order is " + MRT);
}
let L = [ 2, 5, 4 ];
let n = L.length;
findOrderMRT(L, n);
</script>
|
OutputOptimal order in which programs are to bestored is: 2 4 5
Minimum Retrieval Time of this order is 6.33333
Time complexity of the above program is the time complexity for sorting, that is 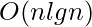 (Since std::sort() operates in
(Since std::sort() operates in 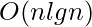 ) If you use bubble sort instead of std::sort(), it will take
) If you use bubble sort instead of std::sort(), it will take 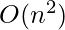
You may think that the time complexity for this particular above code should be due to both the loops in ‘mrt’ calculation, that is,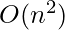 , but do remember that intuitively, the for loops used can also be coded in this manner to avoid two loops :
, but do remember that intuitively, the for loops used can also be coded in this manner to avoid two loops :
for (int i = 0; i < n; i++)
MRT += (n - i) * L[i];
Space complexity: O(n)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...