Operator grammar and precedence parser in TOC
Last Updated :
11 May, 2023
A grammar that is used to define mathematical operators is called an operator grammar or operator precedence grammar. Such grammars have the restriction that no production has either an empty right-hand side (null productions) or two adjacent non-terminals in its right-hand side. Examples – This is an example of operator grammar:
E->E+E/E*E/id
However, the grammar given below is not an operator grammar because two non-terminals are adjacent to each other:
S->SAS/a
A->bSb/b
We can convert it into an operator grammar, though:
S->SbSbS/SbS/a
A->bSb/b
Operator precedence parser – An operator precedence parser is a bottom-up parser that interprets an operator grammar. This parser is only used for operator grammars. Ambiguous grammars are not allowed in any parser except operator precedence parser. There are two methods for determining what precedence relations should hold between a pair of terminals:
- Use the conventional associativity and precedence of operator.
- The second method of selecting operator-precedence relations is first to construct an unambiguous grammar for the language, a grammar that reflects the correct associativity and precedence in its parse trees.
This parser relies on the following three precedence relations: ⋖, ≐, ⋗ a ⋖ b This means a “yields precedence to” b. a ⋗ b This means a “takes precedence over” b. a ≐ b This means a “has same precedence as” b.  Figure – Operator precedence relation table for grammar E->E+E/E*E/id There is not given any relation between id and id as id will not be compared and two variables can not come side by side. There is also a disadvantage of this table – if we have n operators then size of table will be n*n and complexity will be 0(n2). In order to decrease the size of table, we use operator function table. Operator precedence parsers usually do not store the precedence table with the relations; rather they are implemented in a special way. Operator precedence parsers use precedence functions that map terminal symbols to integers, and the precedence relations between the symbols are implemented by numerical comparison. The parsing table can be encoded by two precedence functions f and g that map terminal symbols to integers. We select f and g such that:
Figure – Operator precedence relation table for grammar E->E+E/E*E/id There is not given any relation between id and id as id will not be compared and two variables can not come side by side. There is also a disadvantage of this table – if we have n operators then size of table will be n*n and complexity will be 0(n2). In order to decrease the size of table, we use operator function table. Operator precedence parsers usually do not store the precedence table with the relations; rather they are implemented in a special way. Operator precedence parsers use precedence functions that map terminal symbols to integers, and the precedence relations between the symbols are implemented by numerical comparison. The parsing table can be encoded by two precedence functions f and g that map terminal symbols to integers. We select f and g such that:
- f(a) < g(b) whenever a yields precedence to b
- f(a) = g(b) whenever a and b have the same precedence
- f(a) > g(b) whenever a takes precedence over b
Example – Consider the following grammar:
E -> E + E/E * E/( E )/id
This is the directed graph representing the precedence function: 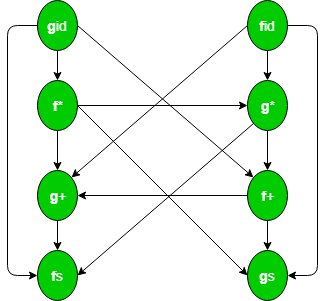 Since there is no cycle in the graph, we can make this function table:
Since there is no cycle in the graph, we can make this function table: 
fid -> g* -> f+ ->g+ -> f$
gid -> f* -> g* ->f+ -> g+ ->f$
Size of the table is 2n. One disadvantage of function tables is that even though we have blank entries in relation table we have non-blank entries in function table. Blank entries are also called error. Hence error detection capability of relation table is greater than function table.
C
#include<stdlib.h>
#include<stdio.h>
#include<string.h>
void f()
{
printf("Not operator grammar");
exit(0);
}
void main()
{
char grm[20][20], c;
int i, n, j = 2, flag = 0;
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%s", grm[i]);
for (i = 0; i < n; i++) {
c = grm[i][2];
while (c != '\0') {
if (grm[i][3] == '+' || grm[i][3] == '-'
|| grm[i][3] == '*' || grm[i][3] == '/')
flag = 1;
else {
flag = 0;
f();
}
if (c == '$') {
flag = 0;
f();
}
c = grm[i][++j];
}
}
if (flag == 1)
printf("Operator grammar");
}
|
Input :3
A=A*A
B=AA
A=$
Output : Not operator grammar
Input :2
A=A/A
B=A+A
Output : Operator grammar
$ is a null production here which are also not allowed in operator grammars. Advantages –
- It can easily be constructed by hand.
- It is simple to implement this type of parsing.
Efficient parsing: Precedence parsers can parse operator grammars in linear time, making them much more efficient than other parsing techniques.
Easy to implement: Operator grammars are relatively easy to define and implement, making them a popular choice for describing the syntax of programming languages.
Improved readability: Using operator precedence parsing can make the syntax of a programming language more readable and easier to understand, as operators can be grouped according to their precedence levels.
Error detection: Precedence parsers can detect certain types of errors, such as syntax errors and operator precedence errors, which can help programmers to debug their code more easily.
Flexibility: Operator grammars and precedence parsers are very flexible, allowing for a wide range of syntax structures to be described, including those with complex operator precedence rules.
Modular design: Precedence parsers can be designed to work with other parsing techniques, such as top-down and bottom-up parsers, allowing for a modular design that can be easily extended or modified.
Disadvantages –
- It is hard to handle tokens like the minus sign (-), which has two different precedence (depending on whether it is unary or binary).
- It is applicable only to a small class of grammars.
Features:
Operator Grammar:
Operators with Precedence: An operator grammar includes operators with different levels of precedence and associativity. The grammar specifies the syntactic structure of expressions, which can be used to derive parse trees for expressions.
Priority and Associativity: Operator grammar provides a way to define the priority and associativity of operators, which is essential for parsing expressions correctly.
Easy to Read: Operator grammar is easy to read and understand, making it a popular choice for designing the syntax of programming languages.
Ambiguity Resolution: Operator grammar helps to reduce ambiguity in expressions by specifying the order in which operators are applied.
Precedence Parser:
Efficient Parsing: Precedence parser can parse expressions efficiently and without requiring backtracking, which makes it faster than other parsing techniques.
Bottom-Up Parsing: Precedence parser is a bottom-up parser that can handle operator precedence and associativity.
Error Recovery: Precedence parser can perform error recovery by detecting errors in expressions and skipping over them to continue parsing the remaining input.
Flexible: Precedence parser can handle a wide range of grammars and can be easily extended to handle new operators or operators with different precedence levels.
Share your thoughts in the comments
Please Login to comment...