Banker’s Algorithm in Operating System
Last Updated :
27 Sep, 2023
The banker’s algorithm is a resource allocation and deadlock avoidance algorithm that tests for safety by simulating the allocation for the predetermined maximum possible amounts of all resources, then makes an “s-state” check to test for possible activities, before deciding whether allocation should be allowed to continue.
Why Banker’s Algorithm is Named So?
The banker’s algorithm is named so because it is used in the banking system to check whether a loan can be sanctioned to a person or not. Suppose there are n number of account holders in a bank and the total sum of their money is S. If a person applies for a loan then the bank first subtracts the loan amount from the total money that the bank has and if the remaining amount is greater than S then only the loan is sanctioned. It is done because if all the account holders come to withdraw their money then the bank can easily do it.
It also helps the OS to successfully share the resources between all the processes. It is called the banker’s algorithm because bankers need a similar algorithm- they admit loans that collectively exceed the bank’s funds and then release each borrower’s loan in installments. The banker’s algorithm uses the notation of a safe allocation state to ensure that granting a resource request cannot lead to a deadlock either immediately or in the future.
In other words, the bank would never allocate its money in such a way that it can no longer satisfy the needs of all its customers. The bank would try to be in a safe state always.
The following Data structures are used to implement the Banker’s Algorithm:
Let ‘n’ be the number of processes in the system and ‘m’ be the number of resource types.
Available
- It is a 1-d array of size ‘m’ indicating the number of available resources of each type.
- Available[ j ] = k means there are ‘k’ instances of resource type Rj
Max
- It is a 2-d array of size ‘n*m’ that defines the maximum demand of each process in a system.
- Max[ i, j ] = k means process Pi may request at most ‘k’ instances of resource type Rj.
Allocation
- It is a 2-d array of size ‘n*m’ that defines the number of resources of each type currently allocated to each process.
- Allocation[ i, j ] = k means process Pi is currently allocated ‘k’ instances of resource type Rj
Need
- It is a 2-d array of size ‘n*m’ that indicates the remaining resource need of each process.
- Need [ i, j ] = k means process Pi currently needs ‘k’ instances of resource type Rj
- Need [ i, j ] = Max [ i, j ] – Allocation [ i, j ]
Allocation specifies the resources currently allocated to process Pi and Needi specifies the additional resources that process Pi may still request to complete its task.
Banker’s algorithm consists of a Safety algorithm and a Resource request algorithm.
Banker’s Algorithm
1. Active:= Running U Blocked;
for k=1…r
New_ request[k]:= Requested_ resources[requesting_ process, k];
2. Simulated_ allocation:= Allocated_ resources;
for k=1…..r //Compute projected allocation state
Simulated_ allocation [requesting _process, k]:= Simulated_ allocation [requesting _process, k] + New_ request[k];
3. feasible:= true;
for k=1….r // Check whether projected allocation state is feasible
if Total_ resources[k]< Simulated_ total_ alloc [k] then feasible:= false;
4. if feasible= true
then // Check whether projected allocation state is a safe allocation state
while set Active contains a process P1 such that
For all k, Total _resources[k] – Simulated_ total_ alloc[k]>= Max_ need [l ,k]-Simulated_ allocation[l, k]
Delete Pl from Active;
for k=1…..r
Simulated_ total_ alloc[k]:= Simulated_ total_ alloc[k]- Simulated_ allocation[l, k];
5. If set Active is empty
then // Projected allocation state is a safe allocation state
for k=1….r // Delete the request from pending requests
Requested_ resources[requesting_ process, k]:=0;
for k=1….r // Grant the request
Allocated_ resources[requesting_ process, k]:= Allocated_ resources[requesting_ process, k] + New_ request[k];
Total_ alloc[k]:= Total_ alloc[k] + New_ request[k];
Safety Algorithm
The algorithm for finding out whether or not a system is in a safe state can be described as follows:
1) Let Work and Finish be vectors of length ‘m’ and ‘n’ respectively.
Initialize: Work = Available
Finish[i] = false; for i=1, 2, 3, 4….n
2) Find an i such that both
a) Finish[i] = false
b) Needi <= Work
if no such i exists goto step (4)
3) Work = Work + Allocation[i]
Finish[i] = true
goto step (2)
4) if Finish [i] = true for all i
then the system is in a safe state
Resource-Request Algorithm
Let Requesti be the request array for process Pi. Requesti [j] = k means process Pi wants k instances of resource type Rj. When a request for resources is made by process Pi, the following actions are taken:
1) If Requesti <= Needi
Goto step (2) ; otherwise, raise an error condition, since the process has exceeded its maximum claim.
2) If Requesti <= Available
Goto step (3); otherwise, Pi must wait, since the resources are not available.
3) Have the system pretend to have allocated the requested resources to process Pi by modifying the state as
follows:
Available = Available – Requesti
Allocationi = Allocationi + Requesti
Needi = Needi– Requesti
Example:
Considering a system with five processes P0 through P4 and three resources of type A, B, C. Resource type A has 10 instances, B has 5 instances and type C has 7 instances. Suppose at time t0 following snapshot of the system has been taken:

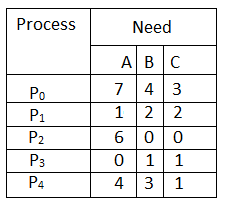
Q.1: What will be the content of the Need matrix?
Need [i, j] = Max [i, j] – Allocation [i, j]
So, the content of Need Matrix is:
Q.2: Is the system in a safe state? If Yes, then what is the safe sequence?
Applying the Safety algorithm on the given system,

Q.3: What will happen if process P1 requests one additional instance of resource type A and two instances of resource type C?

We must determine whether this new system state is safe. To do so, we again execute Safety algorithm on the above data structures.

Hence the new system state is safe, so we can immediately grant the request for process P1 .
Code for Banker’s Algorithm
C++
#include <iostream>
using namespace std;
int main()
{
int n, m, i, j, k;
n = 5;
m = 3;
int alloc[5][3] = { { 0, 1, 0 },
{ 2, 0, 0 },
{ 3, 0, 2 },
{ 2, 1, 1 },
{ 0, 0, 2 } };
int max[5][3] = { { 7, 5, 3 },
{ 3, 2, 2 },
{ 9, 0, 2 },
{ 2, 2, 2 },
{ 4, 3, 3 } };
int avail[3] = { 3, 3, 2 };
int f[n], ans[n], ind = 0;
for (k = 0; k < n; k++) {
f[k] = 0;
}
int need[n][m];
for (i = 0; i < n; i++) {
for (j = 0; j < m; j++)
need[i][j] = max[i][j] - alloc[i][j];
}
int y = 0;
for (k = 0; k < 5; k++) {
for (i = 0; i < n; i++) {
if (f[i] == 0) {
int flag = 0;
for (j = 0; j < m; j++) {
if (need[i][j] > avail[j]){
flag = 1;
break;
}
}
if (flag == 0) {
ans[ind++] = i;
for (y = 0; y < m; y++)
avail[y] += alloc[i][y];
f[i] = 1;
}
}
}
}
int flag = 1;
for(int i = 0;i<n;i++)
{
if(f[i]==0)
{
flag = 0;
cout << "The given sequence is not safe";
break;
}
}
if(flag==1)
{
cout << "Following is the SAFE Sequence" << endl;
for (i = 0; i < n - 1; i++)
cout << " P" << ans[i] << " ->";
cout << " P" << ans[n - 1] <<endl;
}
return (0);
}
|
C
#include <stdio.h>
int main()
{
int n, m, i, j, k;
n = 5;
m = 3;
int alloc[5][3] = { { 0, 1, 0 },
{ 2, 0, 0 },
{ 3, 0, 2 },
{ 2, 1, 1 },
{ 0, 0, 2 } };
int max[5][3] = { { 7, 5, 3 },
{ 3, 2, 2 },
{ 9, 0, 2 },
{ 2, 2, 2 },
{ 4, 3, 3 } };
int avail[3] = { 3, 3, 2 };
int f[n], ans[n], ind = 0;
for (k = 0; k < n; k++) {
f[k] = 0;
}
int need[n][m];
for (i = 0; i < n; i++) {
for (j = 0; j < m; j++)
need[i][j] = max[i][j] - alloc[i][j];
}
int y = 0;
for (k = 0; k < 5; k++) {
for (i = 0; i < n; i++) {
if (f[i] == 0) {
int flag = 0;
for (j = 0; j < m; j++) {
if (need[i][j] > avail[j]){
flag = 1;
break;
}
}
if (flag == 0) {
ans[ind++] = i;
for (y = 0; y < m; y++)
avail[y] += alloc[i][y];
f[i] = 1;
}
}
}
}
int flag = 1;
for(int i=0;i<n;i++)
{
if(f[i]==0)
{
flag=0;
printf("The following system is not safe");
break;
}
}
if(flag==1)
{
printf("Following is the SAFE Sequence\n");
for (i = 0; i < n - 1; i++)
printf(" P%d ->", ans[i]);
printf(" P%d", ans[n - 1]);
}
return (0);
}
|
Java
public class GfGBankers
{
int n = 5;
int m = 3;
int need[][] = new int[n][m];
int [][]max;
int [][]alloc;
int []avail;
int safeSequence[] = new int[n];
void initializeValues()
{
alloc = new int[][] { { 0, 1, 0 },
{ 2, 0, 0 },
{ 3, 0, 2 },
{ 2, 1, 1 },
{ 0, 0, 2 } };
max = new int[][] { { 7, 5, 3 },
{ 3, 2, 2 },
{ 9, 0, 2 },
{ 2, 2, 2 },
{ 4, 3, 3 } };
avail = new int[] { 3, 3, 2 };
}
void isSafe()
{
int count=0;
boolean visited[] = new boolean[n];
for (int i = 0;i < n; i++)
{
visited[i] = false;
}
int work[] = new int[m];
for (int i = 0;i < m; i++)
{
work[i] = avail[i];
}
while (count<n)
{
boolean flag = false;
for (int i = 0;i < n; i++)
{
if (visited[i] == false)
{
int j;
for (j = 0;j < m; j++)
{
if (need[i][j] > work[j])
break;
}
if (j == m)
{
safeSequence[count++]=i;
visited[i]=true;
flag=true;
for (j = 0;j < m; j++)
{
work[j] = work[j]+alloc[i][j];
}
}
}
}
if (flag == false)
{
break;
}
}
if (count < n)
{
System.out.println("The System is UnSafe!");
}
else
{
System.out.println("Following is the SAFE Sequence");
for (int i = 0;i < n; i++)
{
System.out.print("P" + safeSequence[i]);
if (i != n-1)
System.out.print(" -> ");
}
}
}
void calculateNeed()
{
for (int i = 0;i < n; i++)
{
for (int j = 0;j < m; j++)
{
need[i][j] = max[i][j]-alloc[i][j];
}
}
}
public static void main(String[] args)
{
int i, j, k;
GfGBankers gfg = new GfGBankers();
gfg.initializeValues();
gfg.calculateNeed();
gfg.isSafe();
}
}
|
Python3
if __name__=="__main__":
n = 5
m = 3
alloc = [[0, 1, 0 ],[ 2, 0, 0 ],
[3, 0, 2 ],[2, 1, 1] ,[ 0, 0, 2]]
max = [[7, 5, 3 ],[3, 2, 2 ],
[ 9, 0, 2 ],[2, 2, 2],[4, 3, 3]]
avail = [3, 3, 2]
f = [0]*n
ans = [0]*n
ind = 0
for k in range(n):
f[k] = 0
need = [[ 0 for i in range(m)]for i in range(n)]
for i in range(n):
for j in range(m):
need[i][j] = max[i][j] - alloc[i][j]
y = 0
for k in range(5):
for i in range(n):
if (f[i] == 0):
flag = 0
for j in range(m):
if (need[i][j] > avail[j]):
flag = 1
break
if (flag == 0):
ans[ind] = i
ind += 1
for y in range(m):
avail[y] += alloc[i][y]
f[i] = 1
print("Following is the SAFE Sequence")
for i in range(n - 1):
print(" P", ans[i], " ->", sep="", end="")
print(" P", ans[n - 1], sep="")
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int n = 5;
static int m = 3;
int [,]need = new int[n, m];
int [,]max;
int [,]alloc;
int []avail;
int []safeSequence = new int[n];
void initializeValues()
{
alloc = new int[,] {{ 0, 1, 0 },
{ 2, 0, 0 },
{ 3, 0, 2 },
{ 2, 1, 1 },
{ 0, 0, 2 }};
max = new int[,] {{ 7, 5, 3 },
{ 3, 2, 2 },
{ 9, 0, 2 },
{ 2, 2, 2 },
{ 4, 3, 3 }};
avail = new int[] { 3, 3, 2 };
}
void isSafe()
{
int count = 0;
Boolean []visited = new Boolean[n];
for (int i = 0; i < n; i++)
{
visited[i] = false;
}
int []work = new int[m];
for (int i = 0; i < m; i++)
{
work[i] = avail[i];
}
while (count<n)
{
Boolean flag = false;
for (int i = 0; i < n; i++)
{
if (visited[i] == false)
{
int j;
for (j = 0; j < m; j++)
{
if (need[i, j] > work[j])
break;
}
if (j == m)
{
safeSequence[count++] = i;
visited[i] = true;
flag = true;
for (j = 0; j < m; j++)
{
work[j] = work[j] + alloc[i, j];
}
}
}
}
if (flag == false)
{
break;
}
}
if (count < n)
{
Console.WriteLine("The System is UnSafe!");
}
else
{
Console.WriteLine("Following is the SAFE Sequence");
for (int i = 0; i < n; i++)
{
Console.Write("P" + safeSequence[i]);
if (i != n - 1)
Console.Write(" -> ");
}
}
}
void calculateNeed()
{
for (int i = 0;i < n; i++)
{
for (int j = 0;j < m; j++)
{
need[i, j] = max[i, j] - alloc[i, j];
}
}
}
public static void Main(String[] args)
{
GFG gfg = new GFG();
gfg.initializeValues();
gfg.calculateNeed();
gfg.isSafe();
}
}
|
Javascript
<script>
let n, m, i, j, k;
n = 5;
m = 3;
let alloc = [ [ 0, 1, 0 ],
[ 2, 0, 0 ],
[ 3, 0, 2 ],
[ 2, 1, 1 ],
[ 0, 0, 2 ] ];
let max = [ [ 7, 5, 3 ],
[ 3, 2, 2 ],
[ 9, 0, 2 ],
[ 2, 2, 2 ],
[ 4, 3, 3 ] ];
let avail = [ 3, 3, 2 ];
let f = [], ans = [], ind = 0;
for (k = 0; k < n; k++) {
f[k] = 0;
}
let need = [];
for (i = 0; i < n; i++) {
let need1 = [];
for (j = 0; j < m; j++)
need1.push(max[i][j] - alloc[i][j]);
need.push(need1);
}
let y = 0;
for (k = 0; k < 5; k++) {
for (i = 0; i < n; i++) {
if (f[i] == 0) {
let flag = 0;
for (j = 0; j < m; j++) {
if (need[i][j] > avail[j]){
flag = 1;
break;
}
}
if (flag == 0) {
ans[ind++] = i;
for (y = 0; y < m; y++)
avail[y] += alloc[i][y];
f[i] = 1;
}
}
}
}
document.write("Following is the SAFE Sequence" + "<br>");
for (i = 0; i < n - 1; i++)
document.write(" P" + ans[i] + " ->");
document.write( " P" + ans[n - 1] + "<br>");
</script>
|
Output
Following is the SAFE Sequence
P1 -> P3 -> P4 -> P0 -> P2
- As the processes enter the system, they must predict the maximum number of resources needed which is impractical to determine.
- In this algorithm, the number of processes remain fixed which is not possible in interactive systems.
- This algorithm requires that there should be a fixed number of resources to allocate. If a device breaks and becomes suddenly unavailable the algorithm would not work.
- Overhead cost incurred by the algorithm can be high when there are many processes and resources because it has to be invoked for every processes.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...