Prerequisite – Buddy System
Introduction:
Allocating kernel memory is a critical task in operating system design, as the kernel needs to manage memory efficiently and effectively to ensure optimal system performance. Two common methods for allocating kernel memory are the buddy system and the slab system.
The buddy system is a memory allocation algorithm that works by dividing memory into blocks of a fixed size, with each block being a power of two in size. When a request for memory is made, the algorithm finds the smallest available block of memory that is large enough to satisfy the request. If the block is larger than the requested size, it is split into two smaller blocks of equal size (the “buddies”), with each buddy being marked as either allocated or free. The algorithm then continues recursively until it finds the exact size of the requested memory or a block that is the smallest possible size.
The slab system is a memory allocation algorithm that is designed specifically for kernel memory. It works by dividing memory into fixed-size caches or slabs, each of which contains a set of objects of the same type. When a request for memory is made, the algorithm first checks if there is an available object in the appropriate slab cache. If there is, the object is returned. If not, the algorithm allocates a new slab and adds it to the appropriate cache.
The advantages of the buddy system are that it is easy to implement and can handle a wide range of memory sizes. The disadvantages are that it can lead to memory fragmentation and that it can be inefficient for allocating small amounts of memory.
The advantages of the slab system are that it is efficient for allocating small amounts of memory and that it can prevent memory fragmentation. The disadvantages are that it can be more complex to implement than the buddy system and that it may require more memory overhead.
Overall, both the buddy system and the slab system are effective methods for allocating kernel memory, and the choice between the two depends on the specific needs and requirements of the operating system being developed.
Two strategies for managing free memory that is assigned to kernel processes:
1. Buddy system –
Buddy allocation system is an algorithm in which a larger memory block is divided into small parts to satisfy the request. This algorithm is used to give best fit. The two smaller parts of block are of equal size and called as buddies. In the same manner one of the two buddies will further divide into smaller parts until the request is fulfilled. Benefit of this technique is that the two buddies can combine to form the block of larger size according to the memory request.
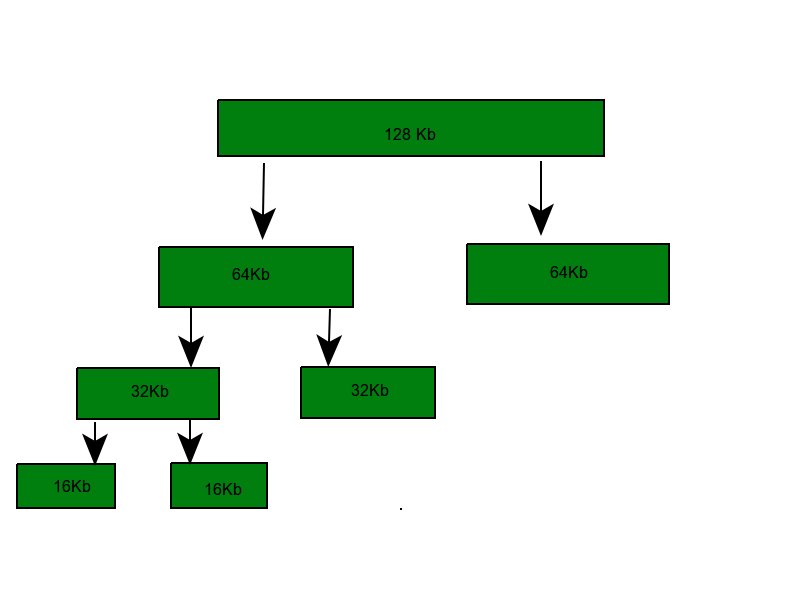
Example – If the request of 25Kb is made then block of size 32Kb is allocated.
Four Types of Buddy System –
- Binary buddy system
- Fibonacci buddy system
- Weighted buddy system
- Tertiary buddy system
Why buddy system?
If the partition size and process size are different then poor match occurs and may use space inefficiently.
It is easy to implement and efficient then dynamic allocation.
Binary buddy system –
The buddy system maintains a list of the free blocks of each size (called a free list), so that it is easy to find a block of the desired size, if one is available. If no block of the requested size is available, Allocate searches for the first non-empty list for blocks of atleast the size requested. In either case, a block is removed from the free list.
Example – Assume the size of memory segment is initially 256kb and the kernel requests 25kb of memory. The segment is initially divided into two buddies. Let we call A1 and A2 each 128kb in size. One of these buddies is further divided into two 64kb buddies let say B1 and B2. But the next highest power of 25kb is 32kb so, either B1 or B2 is further divided into two 32kb buddies(C1 and C2) and finally one of these buddies is used to satisfy the 25kb request. A split block can only be merged with its unique buddy block, which then reforms the larger block they were split from.
Fibonacci buddy system –
This is the system in which blocks are divided into sizes which are Fibonacci numbers. It satisfies the following relation:
Zi = Z(i-1)+Z(i-2)
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 144, 233, 377, 610. The address calculation for the binary and weighted buddy systems is straight forward, but the original procedure for the Fibonacci buddy system was either limited to a small, fixed number of block sizes or a time consuming computation.
Advantages –
- In comparison to other simpler techniques such as dynamic allocation, the buddy memory system has little external fragmentation.
- The buddy memory allocation system is implemented with the use of a binary tree to represent used or unused split memory blocks.
- The buddy system is very fast to allocate or deallocate memory.
- In buddy systems, the cost to allocate and free a block of memory is low compared to that of best-fit or first-fit algorithms.
- Other advantage is coalescing.
- Address calculation is easy.
- Efficient memory management: Kernel memory allocators are designed to efficiently manage memory resources, ensuring that memory is allocated and deallocated in a way that minimizes fragmentation and maximizes available space.
- Customizable allocation policies: Kernel memory allocators can be customized to implement specific allocation policies, such as best fit, worst fit, or first fit. This allows for more precise control over memory usage and allocation.
- High performance: Kernel memory allocators are typically designed for high-performance systems, allowing for fast and efficient allocation and deallocation of memory.
- Reduced memory overhead: Memory allocators can reduce memory overhead by allowing for more efficient use of memory resources, reducing the overall memory footprint of the system.
- Improved system stability: Efficient memory management can help improve system stability by reducing the likelihood of memory leaks, crashes, and other issues related to memory allocation.
Overall, using a kernel memory allocator can help improve system performance, stability, and memory management, making it an essential component of any operating system.
What is coalescing?
It is defined as how quickly adjacent buddies can be combined to form larger segments this is known as coalescing.
For example, when the kernel releases the C1 unit it was allocated, the system can coalesce C1 and C2 into a 64kb segment. This segment B1 can in turn be coalesced with its buddy B2 to form a 128kb segment. Ultimately we can end up with the original 256kb segment.
Drawback –
The main drawback in buddy system is internal fragmentation as larger block of memory is acquired then required. For example if a 36 kb request is made then it can only be satisfied by 64 kb segment and remaining memory is wasted.
2. Slab Allocation –
A second strategy for allocating kernel memory is known as slab allocation. It eliminates fragmentation caused by allocations and deallocations. This method is used to retain allocated memory that contains a data object of a certain type for reuse upon subsequent allocations of objects of the same type. In slab allocation memory chunks suitable to fit data objects of certain type or size are preallocated. Cache does not free the space immediately after use although it keeps track of data which are required frequently so that whenever request is made the data will reach very fast. Two terms required are:
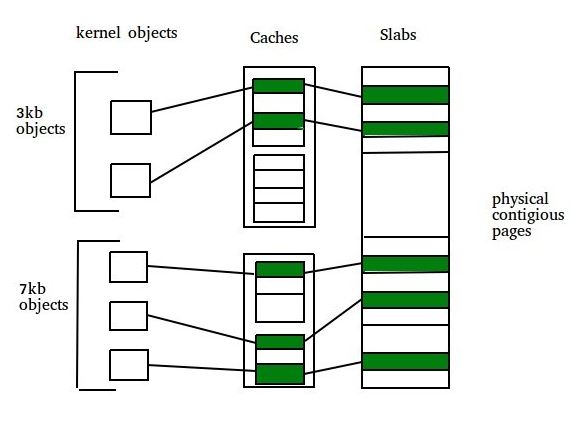
- Slab – A slab is made up of one or more physically contiguous pages. The slab is the actual container of data associated with objects of the specific kind of the containing cache.
- Cache – Cache represents a small amount of very fast memory. A cache consists of one or more slabs. There is a single cache for each unique kernel data structure.
Example –
- A separate cache for a data structure representing processes descriptors
- Separate cache for file objects
- Separate cache for semaphores etc.
Each cache is populated with objects that are instantiations of the kernel data structure the cache represents. For example the cache representing semaphores stores instances of semaphore objects, the cache representing process descriptors stores instances of process descriptor objects.
Implementation –
The slab allocation algorithm uses caches to store kernel objects. When a cache is created a number of objects which are initially marked as free are allocated to the cache. The number of objects in the cache depends on size of the associated slab.
Example – A 12 kb slab (made up of three contiguous 4 kb pages) could store six 2 kb objects. Initially all objects in the cache are marked as free. When a new object for a kernel data structure is needed, the allocator can assign any free object from the cache to satisfy the request. The object assigned from the cache is marked as used.
In linux, a slab may in one of three possible states:
- Full – All objects in the slab are marked as used
- Empty – All objects in the slab are marked as free
- Partial – The slab consists of both
The slab allocator first attempts to satisfy the request with a free object in a partial slab. If none exists, a free object is assigned from an empty slab. If no empty slabs are available, a new slab is allocated from contiguous physical pages and assigned to a cache.
Benefits of slab allocator –
- No memory is wasted due to fragmentation because each unique kernel data structure has an associated cache.
- Memory request can be satisfied quickly.
- The slab allocating scheme is particularly effective for managing when objects are frequently allocated or deallocated. The act of allocating and releasing memory can be a time consuming process. However, objects are created in advance and thus can be quickly allocated from the cache. When the kernel has finished with an object and releases it, it is marked as free and return to its cache, thus making it immediately available for subsequent request from the kernel.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...