numpy.polyint() in Python

numpy.polyint(p, m) : Evaluates the anti - derivative of a polynomial with the specified order. m antiderivative 'P' of polynomial 'p' satisfies

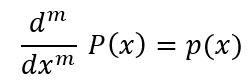
Parameters : p : [array_like or poly1D] polynomial coefficients are given in decreasing order of powers. If the second parameter (root) is set to True then array values are the roots of the polynomial equation. For example, poly1d(3, 2, 6) = 3x² + 2x + 6 m : [int, optional] Order of anti-derivative. Default is 1. Return: Anti-Derivative of the polynomial.

Code #1:

Python3 1==

# Python code explaining  
# numpy.polyint() 
    
# importing libraries 
import numpy as np 
  
# Constructing polynomial  
p1 = np.poly1d([1, 2])  
p2 = np.poly1d([4, 9, 5, 4])  
    
print ("P1 : ", p1)  
print ("\n p2 : \n", p2) 

# Solve for x = 2  
print ("\n\np1 at x = 2 : ", p1(2))  
print ("p2 at x = 2 : ", p2(2))  

a = np.polyint(p1, 1) 
b = np.polyint(p2, 1) 
print ("\n\nUsing polyint") 
print ("p1 anti-derivative of order = 1 : \n", a) 
print ("p2 anti-derivative of order = 1 : \n", b) 

a = np.polyint(p1, 2) 
b = np.polyint(p2, 2) 
print ("\n\nUsing polyint") 
print ("p1 anti-derivative of order = 2 : \n", a) 
print ("p2 anti-derivative of order = 2 : \n", b) 

Output :

P1 :   
1 x + 2

 p2 : 
    3     2
4 x + 9 x + 5 x + 4


p1 at x = 2 :  4
p2 at x = 2 :  82


Using polyint
p1 anti-derivative of order = 1 : 
      2
0.5 x + 2 x
p2 anti-derivative of order = 1 : 
    4     3       2
1 x + 3 x + 2.5 x + 4 x

Code #2:

Python3 1==

# Python code explaining  
# numpy.polyint() 
     
# importing libraries 
import numpy as np 
   
# Constructing polynomial  
p1 = np.poly1d([1, 2])  
p2 = np.poly1d([4, 9, 5, 4])  
   
a = np.polyint(p1, 2) 
b = np.polyint(p2, 2) 

print ("\n\nUsing polyint") 
print ("p1 anti-derivative of order = 2 : \n", a) 
print ("p2 anti-derivative of order = 2 : \n", b) 

Output :

Using polyint
p1 anti-derivative of order = 2 : 
         3     2
0.1667 x + 1 x
p2 anti-derivative of order = 2 : 
      5        4          3     2
0.2 x + 0.75 x + 0.8333 x + 2 x

Create Quiz