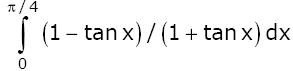Numerical Methods and Calculus

Question 1

Which one of the following functions is continuous at x = 3? 

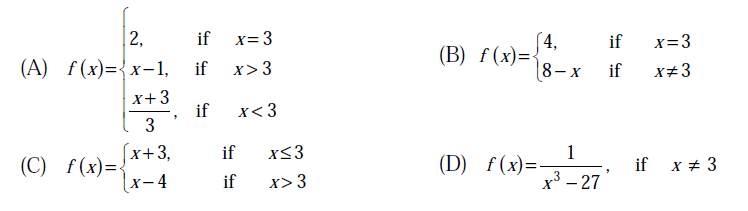[caption width="800"] [/caption]

• C
  

• D
  

• B
  

• A
  

Question 2

Function f is known at the following points: 

• 9.003 
  

• 9.017 
  

• 8.983 
  

• 9.045
  

Question 3

Consider the function f(x) = sin(x) in the interval [π/4, 7π/4]. The number and location(s) of the local minima of this function are

• One, at π/2

• One, at 3π/2

• Two, at π/2 and 3π/2

• Two, at π/4 and 3π/2

Question 4

The bisection method is applied to compute a zero of the function f(x) = x⁴ – x³ – x² – 4 in the 
interval [1,9]. The method converges to a solution after ––––– iterations

• 7
  

• 5
  

• 3
  

• 1
  

Question 5

Given i=√-1, what will be the evaluation of the integral [Tex]\\int_{0}^{\\pi/2} \\frac{\\cos x + i\\sin x}{\\cos x - i\\sin x} dx [/Tex]?

• -i
  

• 2
  

• 0
  

• i
  

Question 6

Newton-Raphson method is used to compute a root of the equation x²-13=0 with 3.5 as the initial value. The approximation after one iteration is

• 3.607
  

• 3.667
  

• 3.676
  

• 3.575
  

Question 7

What is the value of Lim_n->∞(1-1/n)²ⁿ ?

• 1
  

• e^-2
  

• e^-1/2
  

• 0
  

Question 8

Two alternative packages A and B are available for processing a database having 10^k records. Package A requires 0.0001n² time units and package B requires 10nlog₁₀n time units to process n records. What is the smallest value of k for which package B will be preferred over A?

• 12

• 10

• 6

• 5

Question 9

is equivalent to

• 0
• 1
• ln 2
• 1/2 ln 2

Question 10

• 1
• -1
• INF
• -INF