Numbers less than N which are product of exactly two distinct prime numbers
Last Updated :
28 Aug, 2022
Given a number 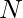 . The task is to find all such numbers less than N and are a product of exactly two distinct prime numbers.
. The task is to find all such numbers less than N and are a product of exactly two distinct prime numbers.
For Example, 33 is the product of two distinct primes i.e 11 * 3, whereas numbers like 60 which has three distinct prime factors i.e 2 * 2 * 3 * 5.
Note: These numbers cannot be a perfect square.
Examples:
Input : N = 30
Output : 6, 10, 14, 15, 21, 22, 26
Input : N = 50
Output : 6, 10, 14, 15, 21, 22, 26, 33, 34, 35, 38, 39, 46
Algorithm:
- Traverse till N and check whether each number has exactly two prime factors or not.
- Now to avoid the situation like 49 having 7 * 7 product of two prime numbers, check whether the number is a perfect square or not to ensure that it has two distinct prime.
- If Step 1 and Step 2 satisfies then add the number in the vector list.
- Traverse the vector and print all the elements in it.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPerfectSquare(long double x)
{
long double sr = sqrt(x);
return ((sr - floor(sr)) == 0);
}
bool isProduct(int num)
{
int cnt = 0;
for (int i = 2; cnt < 2 && i * i <= num; ++i) {
while (num % i == 0) {
num /= i;
++cnt;
}
}
if (num > 1)
++cnt;
return cnt == 2;
}
void findNumbers(int N)
{
vector<int> vec;
for (int i = 1; i <= N; i++) {
if (isProduct(i) && !isPerfectSquare(i)) {
vec.push_back(i);
}
}
for (int i = 0; i < vec.size(); i++) {
cout << vec[i] << " ";
}
}
int main()
{
int N = 30;
findNumbers(N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static boolean isPerfectSquare(double x)
{
double sr = Math.sqrt(x);
return ((sr - Math.floor(sr)) == 0);
}
static boolean isProduct(int num)
{
int cnt = 0;
for (int i = 2; cnt < 2 && i * i <= num; ++i) {
while (num % i == 0) {
num /= i;
++cnt;
}
}
if (num > 1)
++cnt;
return cnt == 2;
}
static void findNumbers(int N)
{
Vector<Integer> vec = new Vector<Integer>();
for (int i = 1; i <= N; i++) {
if (isProduct(i) && !isPerfectSquare(i)) {
vec.add(i);
}
}
Iterator<Integer> itr = vec.iterator();
while(itr.hasNext()){
System.out.print(itr.next()+" ");
}
}
public static void main(String[] args)
{
int N = 30;
findNumbers(N);
}
}
|
Python 3
import math
def isPerfectSquare(x):
sr = math.sqrt(x)
return ((sr - math.floor(sr)) == 0)
def isProduct( num):
cnt = 0
i = 2
while cnt < 2 and i * i <= num:
while (num % i == 0) :
num //= i
cnt += 1
i += 1
if (num > 1):
cnt += 1
return cnt == 2
def findNumbers(N):
vec = []
for i in range(1,N+1) :
if (isProduct(i) and not isPerfectSquare(i)) :
vec.append(i)
for i in range(len( vec)):
print(vec[i] ,end= " ")
if __name__=="__main__":
N = 30
findNumbers(N)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static bool isPerfectSquare(double x)
{
double sr = Math.Sqrt(x);
return ((sr - Math.Floor(sr)) == 0);
}
static bool isProduct(int num)
{
int cnt = 0;
for (int i = 2; cnt < 2 && i * i <= num; ++i)
{
while (num % i == 0)
{
num /= i;
++cnt;
}
}
if (num > 1)
++cnt;
return cnt == 2;
}
static void findNumbers(int N)
{
List<int> vec = new List<int>();
for (int i = 1; i <= N; i++)
{
if (isProduct(i) && !isPerfectSquare(i))
{
vec.Add(i);
}
}
foreach(var a in vec)
Console.Write(a + " ");
}
public static void Main(String[] args)
{
int N = 30;
findNumbers(N);
}
}
|
PHP
<?php
function isPerfectSquare($x)
{
$sr = sqrt($x);
return (($sr - floor($sr)) == 0);
}
function isProduct($num)
{
$cnt = 0;
for ($i = 2; $cnt < 2 &&
$i * $i <= $num; ++$i)
{
while ($num % $i == 0)
{
$num /= $i;
++$cnt;
}
}
if ($num > 1)
++$cnt;
return $cnt == 2;
}
function findNumbers($N)
{
$vec = array();
for ($i = 1; $i <= $N; $i++)
{
if (isProduct($i) &&
!isPerfectSquare($i))
{
array_push($vec, $i);
}
}
for ($i = 0; $i < sizeof($vec); $i++)
{
echo $vec[$i] . " ";
}
}
$N = 30;
findNumbers($N);
|
Javascript
<script>
function isPerfectSquare(x)
{
sr = Math.sqrt(x);
return ((sr - Math.floor(sr)) == 0);
}
function isProduct(num)
{
var cnt = 0;
for(var i = 2; cnt < 2 && (i * i) <= num; ++i)
{
while (num % i == 0)
{
num = parseInt(num / i);
++cnt;
}
}
if (num > 1)
++cnt;
return cnt == 2;
}
function findNumbers( N)
{
vec = [];
for (var i = 1; i <= N; i++)
{
if (isProduct(i) && !isPerfectSquare(i))
{
vec.push(i);
}
}
for (var i = 0; i < vec.length; i++) {
document.write(vec[i] + " ");
}
}
var N = 30;
findNumbers(N);
</script>
|
Output: 6 10 14 15 21 22 26
Time Complexity: O(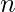 *
*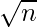 )
)
Auxiliary Space: O(n) , since n extra space has been taken.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...