Number of Pentagons and Hexagons on a Football
Last Updated :
18 Jan, 2023
Given a standard football, regular hexagons and pentagons are drawn on it as shown in the picture. Find out the number of hexagons and pentagons.

We can apply
Euler Characteristics to find out number of Hexagons and Pentagons on a standard Football.
According to Euler Characteristics: For every surface S there exists an integer
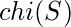
such that whenever a graph G with V vertices and E edges is embedded in S so that there are F faces(regions divided by the graph), we have:
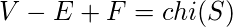
For a sphere(shape of football)
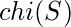
= 2.
Hence, the equation becomes V – E + F = 2.
Now, let number of pentagons P and number of hexagons H.
Number of vertices will be:
6 vertices for each of the hexagons, i.e. 6*H.
5 vertices for each of the pentagons, i.e. 5*P.
But we have counted each vertex thrice, once for each adjacent polygon, follow the picture

Hence, number of vertices, V = (6*H + 5*P)/3.
Number of edges will be:
6 edges for each of the hexagons, i.e. 6*H.
5 edges for each of the pentagons, i.e. 5*P.
But we have counted each edge twice, once for each adjacent polygon, follow the picture

Hence, number of edges, E = (6*H + 5*P)/2.
Number of faces will be:
There are H hexagons and P pentagons, each forming a face. Hence, total number of faces, F = (H + P).
So, we can write:
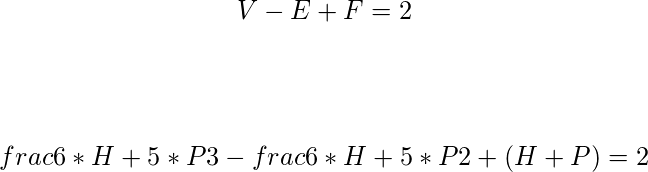
after solving this equation we will get P = 12. So, there are 12 Pentagons.
Now number of Hexagons:
We can see that each pentagon is surrounded by 5 Hexagons. So there should 5*P hexagons, but we have counted each hexagon thrice for each of its 3 adjacent pentagons. Hence, number of hexagons = 5*P/3 = 5*12/3 = 20.
Hence, there are 20 Hexagons and 12 Pentagons in a standard football.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...