Number of ways to swap two bit of s1 so that bitwise OR of s1 and s2 changes
Last Updated :
09 Sep, 2022
Given two binary numbers strings 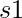 and
and 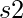 of length
of length 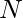 . Find the number of ways of swapping two bits in s1(only s1 not s2) so that bit-wise OR of these two numbers s1 and s2 are changed.
. Find the number of ways of swapping two bits in s1(only s1 not s2) so that bit-wise OR of these two numbers s1 and s2 are changed.
Note: The length of both string must be equal, you can take leading zeros in case of different length.
Example:
Input: s1 = "01011", s2 = "11001"
Output: 4
Explanation:
You can swap the bit of s1 at indexed:
(1, 4), (2, 3), (3, 4) and (3, 5)
there are 4 ways possible.
Input: s1 = "011000", s2 = "010011"
Output: 6
Approach: Initialize a variable result as zero that stores number of ways to swap bits of s1 so that bitwise OR of s1 and s2 changes. Initialize four variables say 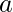 ,
, 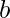 ,
,  , and
, and 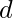 as zero.
as zero.
Traverse both strings from left side and check for the below conditions to increment values of the
variable declared above:
- If the current bit of both s1 and s2 are zero, increment c.
- If current bit of s2 is zero and s1 is one, increment d.
- If current bit of s2 is one and s1 is zero, increment a.
- If current bit of both s1 and s2 is one, increment b.
Update the result by (a*d) + (b*c) + (c*d) and return the result.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
int countWays(string s1, string s2, int n)
{
int a, b, c, d;
a = b = c = d = 0;
int result = 0;
for (int i = 0; i < n; i++) {
if (s2[i] == '0') {
if (s1[i] == '0') {
c++;
}
else {
d++;
}
}
else {
if (s1[i] == '0') {
a++;
}
else {
b++;
}
}
}
result = a * d + b * c + c * d;
return result;
}
int main()
{
int n = 5;
string s1 = "01011";
string s2 = "11001";
cout << countWays(s1, s2, n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int countWays(String s1, String s2, int n)
{
int a, b, c, d;
a = b = c = d = 0;
int result = 0;
for (int i = 0; i < n; i++) {
if (s2.charAt(i) == '0') {
if (s1.charAt(i) == '0') {
c++;
}
else {
d++;
}
}
else {
if (s1.charAt(i) == '0') {
a++;
}
else {
b++;
}
}
}
result = a * d + b * c + c * d;
return result;
}
public static void main (String[] args) {
int n = 5;
String s1 = "01011";
String s2 = "11001";
System.out.println(countWays(s1, s2, n));
}
}
|
Python3
def countWays(s1, s2, n):
a = b = c = d = 0
result = 0;
for i in range(0, n, 1):
if (s2[i] == '0'):
if (s1[i] == '0'):
c += 1;
else:
d += 1
else:
if (s1[i] == '0'):
a += 1
else:
b += 1
result = a * d + b * c + c * d
return result
if __name__ == '__main__':
n = 5
s1 = "01011"
s2 = "11001"
print(countWays(s1, s2, n))
|
C#
using System;
class GFG {
static int countWays(string s1, string s2, int n)
{
int a, b, c, d;
a = b = c = d = 0;
int result = 0;
for (int i = 0; i < n; i++) {
if (s2[i] == '0') {
if (s1[i] == '0') {
c++;
}
else {
d++;
}
}
else {
if (s1[i] == '0') {
a++;
}
else {
b++;
}
}
}
result = a * d + b * c + c * d;
return result;
}
public static void Main () {
int n = 5;
string s1 = "01011";
string s2 = "11001";
Console.WriteLine(countWays(s1, s2, n));
}
}
|
PHP
<?php
function countWays($s1, $s2, $n)
{
$a = $b = $c = $d = 0;
$result = 0;
for ($i = 0; $i < $n; $i++)
{
if ($s2[$i] == '0')
{
if ($s1[$i] == '0')
{
$c++;
}
else
{
$d++;
}
}
else
{
if ($s1[$i] == '0')
{
$a++;
}
else
{
$b++;
}
}
}
$result = $a * $d + $b *
$c + $c * $d;
return $result;
}
$n = 5;
$s1 = "01011";
$s2 = "11001";
echo countWays($s1, $s2, $n);
?>
|
Javascript
<script>
function countWays(s1, s2 , n)
{
var a, b, c, d;
a = b = c = d = 0;
var result = 0;
for (i = 0; i < n; i++) {
if (s2.charAt(i) == '0') {
if (s1.charAt(i) == '0') {
c++;
}
else {
d++;
}
}
else {
if (s1.charAt(i) == '0') {
a++;
}
else {
b++;
}
}
}
result = a * d + b * c + c * d;
return result;
}
var n = 5;
var s1 = "01011";
var s2 = "11001";
document.write(countWays(s1, s2, n));
</script>
|
Complexity y Analysis:
- Time Complexity: O(N)
- Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...