Number of ways to arrange 2*N persons on the two sides of a table with X and Y persons on opposite sides
Last Updated :
06 Mar, 2023
Given three integers N, X and Y. The task is to find the number of ways to arrange 2*N persons along two sides of a table with N number of chairs on each side such that X persons are on one side and Y persons are on the opposite side.
Note: Both X and Y are less than or equals to N.
Examples:
Input : N = 5, X = 4, Y = 2
Output : 57600
Explanation :
The total number of person 10. X men on one side and Y on other side, then 10 – 4 – 2 = 4 persons are left. We can choose 5 – 4 = 1 of them on one side in 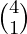 ways and the remaining persons will automatically sit on the other side. On each side arrangement is done in 5! ways. The number of ways is
ways and the remaining persons will automatically sit on the other side. On each side arrangement is done in 5! ways. The number of ways is 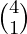 .5!5!
.5!5!
Input : N = 3, X = 1, Y = 2
Output : 108
Approach :
The total number of person 2*N. Let call both the sides as A and B. X men on side A and Y on side B, then 2*N – X – Y persons are left. We can choose N-X of them for side A in 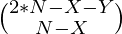 ways and the remaining persons will automatically sit on the other side B. On each side arrangement is done in N! ways. The number of ways to arrange 2*N persons along two sides of a table is
ways and the remaining persons will automatically sit on the other side B. On each side arrangement is done in N! ways. The number of ways to arrange 2*N persons along two sides of a table is 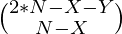 .N!N!
.N!N!
Below is the implementation of the above approach :
C++
#include <bits/stdc++.h>
using namespace std;
int factorial(int n)
{
if (n <= 1)
return 1;
return n * factorial(n - 1);
}
int nCr(int n, int r)
{
return factorial(n) / (factorial(n - r) * factorial(r));
}
int NumberOfWays(int n, int x, int y)
{
return nCr(2*n-x-y, n-x) * factorial(n) * factorial(n);
}
int main()
{
int n = 5, x = 4, y = 2;
cout << NumberOfWays(n, x, y);
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
import java.io.*;
class GFG
{
static int factorial(int n)
{
if (n <= 1)
return 1;
return n * factorial(n - 1);
}
static int nCr(int n, int r)
{
return factorial(n) / (factorial(n - r) *
factorial(r));
}
static int NumberOfWays(int n, int x, int y)
{
return nCr(2 * n - x - y, n - x) *
factorial(n) * factorial(n);
}
public static void main (String[] args)
throws java.lang.Exception
{
int n = 5, x = 4, y = 2;
System.out.println(NumberOfWays(n, x, y));
}
}
|
Python3
def factorial(n):
if (n <= 1):
return 1;
return n * factorial(n - 1);
def nCr(n, r):
return (factorial(n) /
(factorial(n - r) * factorial(r)));
def NumberOfWays(n, x, y):
return (nCr(2 * n - x - y, n - x) *
factorial(n) * factorial(n));
n, x, y = 5, 4, 2;
print(int(NumberOfWays(n, x, y)));
|
C#
using System;
class GFG
{
static int factorial(int n)
{
if (n <= 1)
return 1;
return n * factorial(n - 1);
}
static int nCr(int n, int r)
{
return factorial(n) / (factorial(n - r) *
factorial(r));
}
static int NumberOfWays(int n, int x, int y)
{
return nCr(2 * n - x - y, n - x) *
factorial(n) * factorial(n);
}
public static void Main(String[] args)
{
int n = 5, x = 4, y = 2;
Console.WriteLine(NumberOfWays(n, x, y));
}
}
|
PHP
<?php
function factorial($n)
{
if ($n <= 1)
return 1;
return $n * factorial($n - 1);
}
function nCr($n, $r)
{
return factorial($n) / (factorial($n - $r) *
factorial($r));
}
function NumberOfWays($n, $x, $y)
{
return nCr(2 * $n - $x - $y, $n - $x) *
factorial($n) * factorial($n);
}
$n = 5;
$x = 4;
$y = 2;
echo (NumberOfWays($n, $x, $y));
?>
|
Javascript
<script>
function factorial(n) {
if (n <= 1)
return 1;
return n * factorial(n - 1);
}
function nCr(n , r) {
return factorial(n) / (factorial(n - r) * factorial(r));
}
function NumberOfWays(n , x , y) {
return nCr(2 * n - x - y, n - x) * factorial(n) * factorial(n);
}
var n = 5, x = 4, y = 2;
document.write(NumberOfWays(n, x, y));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(N), for recursive stack space.
Method – 2 O(1) Space Solution
In the above solution, we implemented the factorial function in a recursive manner if we implement the factorial function in an iterative manner then we don’t need O(n) auxiliary extra stack space so this way solution becomes O(1) space complexity solution
Below is an implementation for the same :
C++
#include <bits/stdc++.h>
using namespace std;
int factorial(int n) {
int fact = 1;
for (int i = 1; i <= n; i++) {
fact = fact * i;
}
return fact;
}
int nCr(int n, int r) {
return factorial(n) / (factorial(n - r) * factorial(r));
}
int NumberOfWays(int n, int x, int y) {
return nCr(2 * n - x - y, n - x) * factorial(n) * factorial(n);
}
int main() {
int n = 5, x = 4, y = 2;
cout << NumberOfWays(n, x, y);
return 0;
}
|
Java
public class Main {
public static int factorial(int n) {
int fact = 1;
for (int i = 1; i <= n; i++) {
fact = fact * i;
}
return fact;
}
public static int nCr(int n, int r) {
return factorial(n) / (factorial(n - r) * factorial(r));
}
public static int NumberOfWays(int n, int x, int y) {
return nCr(2 * n - x - y, n - x) * factorial(n) * factorial(n);
}
public static void main(String[] args) {
int n = 5, x = 4, y = 2;
System.out.println(NumberOfWays(n, x, y));
}
}
|
Python3
import math
def factorial(n):
fact = 1
for i in range(1, n+1):
fact = fact * i
return fact
def nCr(n, r):
return factorial(n) // (factorial(n - r) * factorial(r))
def NumberOfWays(n, x, y):
return nCr(2*n - x - y, n - x) * factorial(n) * factorial(n)
n, x, y = 5, 4, 2
print(NumberOfWays(n, x, y))
|
C#
using System;
public class Program {
public static int Factorial(int n) {
int fact = 1;
for (int i = 1; i <= n; i++) {
fact = fact * i;
}
return fact;
}
public static int nCr(int n, int r) {
return Factorial(n) / (Factorial(n - r) * Factorial(r));
}
public static int NumberOfWays(int n, int x, int y) {
return nCr(2 * n - x - y, n - x) * Factorial(n) * Factorial(n);
}
public static void Main() {
int n = 5, x = 4, y = 2;
Console.WriteLine(NumberOfWays(n, x, y));
}
}
|
Javascript
function factorial(n) {
let fact = 1;
for (let i = 1; i <= n; i++) {
fact = fact * i;
}
return fact;
}
function nCr(n, r) {
return factorial(n) / (factorial(n - r) * factorial(r));
}
function numberOfWays(n, x, y) {
return nCr(2 * n - x - y, n - x) * factorial(n) * factorial(n);
}
const n = 5, x = 4, y = 2;
console.log(numberOfWays(n, x, y));
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...