Number of triangles in a plane if no more than two points are collinear
Last Updated :
21 Aug, 2022
Given n points in a plane and no more than two points are collinear, the task is to count the number of triangles in a given plane.
Examples:
Input : n = 3
Output : 1
Input : n = 4
Output : 4

Let there are n points in a plane and no three or more points are collinear then number of triangles in the given plane is given by 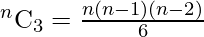
C++
#include <bits/stdc++.h>
using namespace std;
int countNumberOfTriangles(int n)
{
return n * (n - 1) * (n - 2) / 6;
}
int main()
{
int n = 4;
cout << countNumberOfTriangles(n);
return 0;
}
|
C
#include <stdio.h>
int countNumberOfTriangles(int n)
{
return n * (n - 1) * (n - 2) / 6;
}
int main()
{
int n = 4;
printf("%d",countNumberOfTriangles(n));
return 0;
}
|
Java
import java.io.*;
class GFG {
static int countNumberOfTriangles(int n)
{
return n * (n - 1) * (n - 2) / 6;
}
public static void main(String[] args)
{
int n = 4;
System.out.println(
countNumberOfTriangles(n));
}
}
|
Python3
def countNumberOfTriangles(n) :
return (n * (n - 1) *
(n - 2) // 6)
if __name__ == '__main__' :
n = 4
print(countNumberOfTriangles(n))
|
C#
using System;
class GFG
{
static int countNumberOfTriangles(int n)
{
return n * (n - 1) *
(n - 2) / 6;
}
public static void Main()
{
int n = 4;
Console.WriteLine(
countNumberOfTriangles(n));
}
}
|
PHP
<?php
function countNumberOfTriangles($n)
{
return $n * ($n - 1) *
($n - 2) / 6;
}
$n = 4;
echo countNumberOfTriangles($n);
?>
|
Javascript
<script>
function countNumberOfTriangles(n)
{
return n * (n - 1) * (n - 2) / 6;
}
var n = 4;
document.write(countNumberOfTriangles(n));
</script>
|
Time complexity: O(1)
Auxiliary space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...