Number of triangles formed from a set of points on three lines

Given three integers m, n, and k that store the number of points on lines l1, l2, and l3 respectively that do not intersect. The task is to find the number of triangles that can possibly be formed from these set of points.

Examples:

Input: m = 3, n =  4, k = 5 
Output: 205

Input: m = 2, n =  2, k = 1 
Output: 10

Approach:

• The total number of points are (m + n + k) which must give 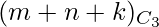number of triangles.
• But ‘m’ points on ‘l1’ gives 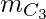combinations that can not form a triangle.
• Similarly, 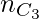and 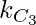number of triangles can not be formed.
• Therefore, Required Number of Triangles = 

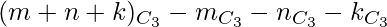
Below is the implementation of the above approach: 

C++

// CPP program to find the possible number
// of triangles that can be formed from
// set of points on three lines
#include <bits/stdc++.h>
using namespace std;

// Returns factorial of a number
int factorial(int n)
{
    int fact = 1;
    for (int i = 2; i <= n; i++)
        fact = fact * i;
    return fact;
}

// calculate c(n, r)
int ncr(int n, int r)
{

    return factorial(n) / (factorial(r) * factorial(n - r));
}

// Driver code
int main()
{
    int m = 3, n = 4, k = 5;
    int totalTriangles = ncr(m + n + k, 3) - ncr(m, 3)
                         - ncr(n, 3) - ncr(k, 3);
    cout << totalTriangles << endl;
}

Java

// Java  program to find the possible number
// of triangles that can be formed from
// set of points on three lines

import java.io.*;

class GFG {

    // Returns factorial of a number
    static int factorial(int n)
    {
        int fact = 1;
        for (int i = 2; i <= n; i++)
            fact = fact * i;
        return fact;
    }

    // calculate c(n, r)
    static int ncr(int n, int r)
    {

        return factorial(n)
            / (factorial(r) * factorial(n - r));
    }

    // Driver code
    public static void main(String[] args)
    {

        int m = 3, n = 4, k = 5;
        int totalTriangles = ncr(m + n + k, 3) - ncr(m, 3)
                             - ncr(n, 3) - ncr(k, 3);
        System.out.println(totalTriangles);
    }
}

Python 3

# Python 3 program to find the
# possible number of triangles
# that can be formed from set of
# points on three lines


# Returns factorial of a number
def factorial(n):
    fact = 1
    for i in range(2, n + 1):
        fact = fact * i
    return fact

# calculate c(n, r)
def ncr(n, r):

    return (factorial(n) // (factorial(r) *
                             factorial(n - r)))

# Driver code
if __name__ == "__main__":
    m = 3
    n = 4
    k = 5
    totalTriangles = (ncr(m + n + k, 3) -
                      ncr(m, 3) - ncr(n, 3) -
                      ncr(k, 3))
    print(totalTriangles)

# This code is contributed
# by ChitraNayal

C#

// C# program to find the possible number
// of triangles that can be formed from
// set of points on three lines
using System;

class GFG
{

// Returns factorial of a number
static int factorial(int n)
{
    int fact = 1;
    for (int i = 2; i <= n; i++)
        fact = fact * i;
    return fact;
}

// calculate c(n, r)
static int ncr(int n, int r)
{

    return factorial(n) / (factorial(r) *
                           factorial(n - r));
}

// Driver code
public static void Main ()
{
    int m = 3, n = 4, k = 5;

    int totalTriangles = ncr(m + n + k, 3) -
                         ncr(m, 3) - ncr(n, 3) -
                         ncr(k, 3);

    Console.WriteLine (totalTriangles);
}
}

// This code is contributed
// by anuj_67..

PHP

<?php
// PHP program to find the possible
// number of triangles that can be
// formed from set of points on
// three lines

// Returns factorial of a number
function factorial($n)
{
    $fact = 1;
    for ($i = 2; $i <= $n; $i++)
        $fact = $fact * $i;
    return $fact;
}

// calculate c(n, r)
function ncr($n, $r)
{
    return factorial($n) / (factorial($r) *
                            factorial($n - $r));
}

// Driver code
$m = 3; $n = 4; $k = 5;
$totalTriangles = ncr($m + $n + $k, 3) -
                  ncr($m, 3) - ncr($n, 3) -
                  ncr($k, 3);
echo $totalTriangles . "\n";

// This code is contributed
// by Akanksha Rai

Javascript

<script>

//JavaScript  program to find the possible number
// of triangles that can be formed from
// set of points on three lines


// Returns factorial of a number
function factorial(n)
{
    var fact = 1;
    for (i = 2; i <= n; i++)
        fact = fact * i;
    return fact;
}

// calculate c(n, r)
function ncr(n , r)
{

    return factorial(n)
        / (factorial(r) * factorial(n - r));
}

// Driver code
var m = 3, n = 4, k = 5;
var totalTriangles = ncr(m + n + k, 3) -
   ncr(m, 3) - ncr(n, 3) - ncr(k, 3);
document.write(totalTriangles);

// This code is contributed by 29AjayKumar

</script>

Output:

205

Time Complexity: O(m + n + k)

Auxiliary Space: O(1)