Number of triangles formed from a set of points on three lines
Last Updated :
25 Jul, 2022
Given three integers m, n, and k that store the number of points on lines l1, l2, and l3 respectively that do not intersect. The task is to find the number of triangles that can possibly be formed from these set of points.
Examples:
Input: m = 3, n = 4, k = 5
Output: 205
Input: m = 2, n = 2, k = 1
Output: 10
Approach:
- The total number of points are (m + n + k) which must give
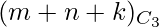 number of triangles.
number of triangles. - But ‘m’ points on ‘l1’ gives
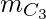 combinations that can not form a triangle.
combinations that can not form a triangle. - Similarly,
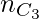 and
and 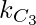 number of triangles can not be formed.
number of triangles can not be formed. - Therefore, Required Number of Triangles =
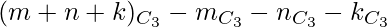
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
int ncr(int n, int r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
int main()
{
int m = 3, n = 4, k = 5;
int totalTriangles = ncr(m + n + k, 3) - ncr(m, 3)
- ncr(n, 3) - ncr(k, 3);
cout << totalTriangles << endl;
}
|
Java
import java.io.*;
class GFG {
static int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
static int ncr(int n, int r)
{
return factorial(n)
/ (factorial(r) * factorial(n - r));
}
public static void main(String[] args)
{
int m = 3, n = 4, k = 5;
int totalTriangles = ncr(m + n + k, 3) - ncr(m, 3)
- ncr(n, 3) - ncr(k, 3);
System.out.println(totalTriangles);
}
}
|
Python 3
def factorial(n):
fact = 1
for i in range(2, n + 1):
fact = fact * i
return fact
def ncr(n, r):
return (factorial(n) // (factorial(r) *
factorial(n - r)))
if __name__ == "__main__":
m = 3
n = 4
k = 5
totalTriangles = (ncr(m + n + k, 3) -
ncr(m, 3) - ncr(n, 3) -
ncr(k, 3))
print(totalTriangles)
|
C#
using System;
class GFG
{
static int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
static int ncr(int n, int r)
{
return factorial(n) / (factorial(r) *
factorial(n - r));
}
public static void Main ()
{
int m = 3, n = 4, k = 5;
int totalTriangles = ncr(m + n + k, 3) -
ncr(m, 3) - ncr(n, 3) -
ncr(k, 3);
Console.WriteLine (totalTriangles);
}
}
|
PHP
<?php
function factorial($n)
{
$fact = 1;
for ($i = 2; $i <= $n; $i++)
$fact = $fact * $i;
return $fact;
}
function ncr($n, $r)
{
return factorial($n) / (factorial($r) *
factorial($n - $r));
}
$m = 3; $n = 4; $k = 5;
$totalTriangles = ncr($m + $n + $k, 3) -
ncr($m, 3) - ncr($n, 3) -
ncr($k, 3);
echo $totalTriangles . "\n";
|
Javascript
<script>
function factorial(n)
{
var fact = 1;
for (i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
function ncr(n , r)
{
return factorial(n)
/ (factorial(r) * factorial(n - r));
}
var m = 3, n = 4, k = 5;
var totalTriangles = ncr(m + n + k, 3) -
ncr(m, 3) - ncr(n, 3) - ncr(k, 3);
document.write(totalTriangles);
</script>
|
Time Complexity: O(m + n + k)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...