Number of Subsequences with Even and Odd Sum | Set 2
Last Updated :
19 Sep, 2023
Given an array arr[] of size N. The task is to find the number of subsequences whose sum is even and the number of subsequences whose sum is odd.
Examples:
Input: arr[] = {1, 2, 2, 3}
Output: EvenSum = 7, OddSum = 8
There are 2N-1 possible subsequences.
The subsequences with even sum are
1) {1, 3} Sum = 4
2) {1, 2, 2, 3} Sum = 8
3) {1, 2, 3} Sum = 6 (Of index 1)
4) {1, 2, 3} Sum = 6 (Of index 2)
5) {2} Sum = 2 (Of index 1)
6) {2, 2} Sum = 4
7) {2} Sum = 2 (Of index 2)
and the rest subsequence is of odd sum.
Input: arr[] = { 2, 2, 2, 2 }
Output: EvenSum = 15, OddSum = 0
Approach: This article already exists here having time complexity of 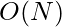 where N is the size of array. Visit here before moving further.
where N is the size of array. Visit here before moving further.
- If we can find the number of odd subsequences then we can easily find the number of even subsequences.
- The odd subsequences can be formed in two ways:
- By taking odd number odd times.
- Taking even number and odd number odd time.
- Below are some variables and their definition:
- N = Total number of element in the array.
- Even = Total number of evens in the array.
- Odd = Total number of odd in the array.
- Tseq = Total number of subsequences.
- Oseq = Total number of subsequences with only odd number.
- Eseq = Total number of subsequences with even number.
- OddSumSeq = Total number of subsequences with odd sum.
- EvenSumSeq = Total number of subsequences with even sum.
Tseq = 2N – 1 = Even Subsequence + OddSubsequence
Eseq = 2Even
Oseq = OddC1 + OddC3 + OddC5 + . . . .
where OddC1 = Choosing 1 Odd
OddC3 = Choosing 3 Odd and so on
We can reduce the above equation by this identity, Hence
Oseq = 2Odd – 1
So, hence for the total odd sum subsequence, it can be calculated by multiplying these above result
OddSumSeq = 2Even * 2Odd – 1
EvenSumSeq = 2N – 1 – OddSumSeq
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
pair<int, int> countSum(int arr[], int n)
{
int NumberOfOdds = 0, NumberOfEvens = 0;
for (int i = 0; i < n; i++)
if (arr[i] & 1)
NumberOfOdds++;
NumberOfEvens = n - NumberOfOdds;
int NumberOfOddSubsequences = (1 << NumberOfEvens)
* (1 << (NumberOfOdds - 1));
int NumberOfEvenSubsequences = (1 << n) - 1
- NumberOfOddSubsequences;
return { NumberOfEvenSubsequences,
NumberOfOddSubsequences };
}
int main()
{
int arr[] = { 1, 2, 2, 3 };
int n = sizeof(arr) / sizeof(arr[0]);
pair<int, int> ans = countSum(arr, n);
cout << "EvenSum = " << ans.first;
cout << " OddSum = " << ans.second;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static class pair
{
int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
static pair countSum(int arr[], int n)
{
int NumberOfOdds = 0, NumberOfEvens = 0;
for (int i = 0; i < n; i++)
if (arr[i] % 2 == 1)
NumberOfOdds++;
NumberOfEvens = n - NumberOfOdds;
int NumberOfOddSubsequences = (1 << NumberOfEvens) *
(1 << (NumberOfOdds - 1));
int NumberOfEvenSubsequences = (1 << n) - 1 -
NumberOfOddSubsequences;
return new pair(NumberOfEvenSubsequences,
NumberOfOddSubsequences);
}
public static void main(String[] args)
{
int arr[] = { 1, 2, 2, 3 };
int n = arr.length;
pair ans = countSum(arr, n);
System.out.print("EvenSum = " + ans.first);
System.out.print(" OddSum = " + ans.second);
}
}
|
Python3
def countSum(arr, n) :
NumberOfOdds = 0; NumberOfEvens = 0;
for i in range(n) :
if (arr[i] & 1) :
NumberOfOdds += 1;
NumberOfEvens = n - NumberOfOdds;
NumberOfOddSubsequences = (1 << NumberOfEvens) * \
(1 << (NumberOfOdds - 1));
NumberOfEvenSubsequences = (1 << n) - 1 - \
NumberOfOddSubsequences;
return (NumberOfEvenSubsequences,
NumberOfOddSubsequences);
if __name__ == "__main__":
arr = [ 1, 2, 2, 3 ];
n = len(arr);
ans = countSum(arr, n);
print("EvenSum =", ans[0], end = " ");
print("OddSum =", ans[1]);
|
C#
using System;
class GFG
{
public class pair
{
public int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
static pair countSum(int []arr, int n)
{
int NumberOfOdds = 0, NumberOfEvens = 0;
for (int i = 0; i < n; i++)
if (arr[i] % 2 == 1)
NumberOfOdds++;
NumberOfEvens = n - NumberOfOdds;
int NumberOfOddSubsequences = (1 << NumberOfEvens) *
(1 << (NumberOfOdds - 1));
int NumberOfEvenSubsequences = (1 << n) - 1 -
NumberOfOddSubsequences;
return new pair(NumberOfEvenSubsequences,
NumberOfOddSubsequences);
}
public static void Main(String[] args)
{
int []arr = { 1, 2, 2, 3 };
int n = arr.Length;
pair ans = countSum(arr, n);
Console.Write("EvenSum = " + ans.first);
Console.Write(" OddSum = " + ans.second);
}
}
|
Javascript
<script>
function countSum(arr, n) {
let NumberOfOdds = 0, NumberOfEvens = 0;
for (let i = 0; i < n; i++)
if (arr[i] & 1)
NumberOfOdds++;
NumberOfEvens = n - NumberOfOdds;
let NumberOfOddSubsequences = (1 << NumberOfEvens)
* (1 << (NumberOfOdds - 1));
let NumberOfEvenSubsequences = (1 << n) - 1
- NumberOfOddSubsequences;
return [NumberOfEvenSubsequences,
NumberOfOddSubsequences];
}
let arr = [1, 2, 2, 3];
let n = arr.length;
let ans = countSum(arr, n);
document.write("EvenSum = " + ans[0]);
document.write(" OddSum = " + ans[1]);
</script>
|
Output: EvenSum = 7 OddSum = 8
Time Complexity: O(n)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...