Number of strictly increasing Buildings from right with distinct Colors
Last Updated :
31 May, 2022
Given an integer 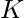 and two integer arrays H[] and C[] of size
and two integer arrays H[] and C[] of size 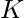 where H[] stores the height of consecutive buildings and C[] stores the color codes for those building in which they are painted.
where H[] stores the height of consecutive buildings and C[] stores the color codes for those building in which they are painted.
The task is to determine how many colors are visible at once from the view on the right i.e. right of the rightmost building.
Examples:
Input: K = 5, H[] = {5, 4, 3, 2, 3}, C[] = {1, 2, 3, 4, 5}
Output: 3

Input: K = 5, H[] = {1, 2, 3, 4, 5}, C[] = {3, 3, 3, 3, 3}
Output: 1
Approach: On observing carefully, the above problem can be simplified to find the number of strictly increasing buildings from right with distinct colors.
- Store the Last element of Height array in max variable.
- Now in an array Arr, at position corresponding to the element at the last of the colour array store 1.
- Now start traversing the Height array from n-2 to 0.
- If we get element greater than max then store that variable in max and again in array Arr, at position correspond to the ith element in the colour array store 1.
- At last Count the number of 1’s present in the array Arr. It gives the total number of colour visible from the end.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int colourVisible(int height[], int colour[], int K)
{
int arr[K + 1] = { 0 }, visible = 0;
int max = height[K - 1];
arr[colour[K - 1]] = 1;
for (int i = K - 2; i >= 0; i--) {
if (height[i] > max) {
max = height[i];
arr[colour[i]] = 1;
}
}
for (int i = 1; i <= K; i++) {
if (arr[i] == 1)
visible++;
}
return visible;
}
int main()
{
int height[] = { 3, 5, 1, 2, 3 };
int colour[] = { 1, 2, 3, 4, 3 };
int K = sizeof(colour) / sizeof(colour[0]);
cout << colourVisible(height, colour, K);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int colourVisible(int height[], int colour[], int K)
{
int arr[]=new int[K + 1] ;
int visible = 0;
int max = height[K - 1];
arr[colour[K - 1]] = 1;
for (int i = K - 2; i >= 0; i--) {
if (height[i] > max) {
max = height[i];
arr[colour[i]] = 1;
}
}
for (int i = 1; i <= K; i++) {
if (arr[i] == 1)
visible++;
}
return visible;
}
public static void main (String[] args) {
int height[] = { 3, 5, 1, 2, 3 };
int colour[] = { 1, 2, 3, 4, 3 };
int K = colour.length;
System.out.println (colourVisible(height, colour, K));
}
}
|
Python3
def colourVisible(height, colour, K):
arr = [0 for i in range(K + 1)]
visible = 0
max = height[K - 1]
arr[colour[K - 1]] = 1
i = K - 2
while(i >= 0):
if (height[i] > max):
max = height[i]
arr[colour[i]] = 1
i -= 1
for i in range(1, K + 1, 1):
if (arr[i] == 1):
visible += 1
return visible
if __name__ == '__main__':
height = [3, 5, 1, 2, 3]
colour = [1, 2, 3, 4, 3]
K = len(colour)
print(colourVisible(height, colour, K))
|
C#
using System;
class GFG
{
static int colourVisible(int []height,
int []colour, int K)
{
int []arr=new int[K + 1] ;
int visible = 0;
int max = height[K - 1];
arr[colour[K - 1]] = 1;
for (int i = K - 2; i >= 0; i--)
{
if (height[i] > max)
{
max = height[i];
arr[colour[i]] = 1;
}
}
for (int i = 1; i <= K; i++)
{
if (arr[i] == 1)
visible++;
}
return visible;
}
static public void Main ()
{
int []height = { 3, 5, 1, 2, 3 };
int []colour = { 1, 2, 3, 4, 3 };
int K = colour.Length;
Console.WriteLine(colourVisible(height, colour, K));
}
}
|
PHP
<?php
function colourVisible($height, $colour, $K)
{
$arr = array_fill(0, $K + 1, 0);
$visible = 0;
$max = $height[$K - 1];
$arr[$colour[$K - 1]] = 1;
for ($i = $K - 2; $i >= 0; $i--)
{
if ($height[$i] > $max)
{
$max = $height[$i];
$arr[$colour[$i]] = 1;
}
}
for ($i = 1; $i <= $K; $i++)
{
if ($arr[$i] == 1)
$visible++;
}
return $visible;
}
$height = array( 3, 5, 1, 2, 3 );
$colour = array( 1, 2, 3, 4, 3 );
$K = count($colour);
echo colourVisible($height, $colour, $K);
?>
|
Javascript
<script>
function colourVisible(height, colour, K)
{
var arr = Array(K+1).fill(0), visible = 0;
var max = height[K - 1];
arr[colour[K - 1]] = 1;
for (var i = K - 2; i >= 0; i--) {
if (height[i] > max) {
max = height[i];
arr[colour[i]] = 1;
}
}
for (var i = 1; i <= K; i++) {
if (arr[i] == 1)
visible++;
}
return visible;
}
var height = [ 3, 5, 1, 2, 3 ];
var colour = [ 1, 2, 3, 4, 3 ];
var K = colour.length;
document.write( colourVisible(height, colour, K));
</script>
|
Time Complexity: O(K), where K is the size of colour array
Auxiliary Space: O(K), as an extra size of K is used
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...