Number of relations that are neither Reflexive nor Irreflexive on a Set
Last Updated :
13 Oct, 2022
Given a positive integer N, the task is to find the number of relations that are neither reflexive nor irreflexive on a set of first N natural numbers. Since the count of relations can be very large, print it to modulo 109 + 7.
A relation R on a set A is called reflexive, if no (a, a) € R holds for every element a € A.
For Example: If set A = {a, b} then R = {(a, b), (b, a)} is irreflexive relation.
Examples:
Input: N = 2
Output: 8
Explanation: Considering the set {1, 2}, the total possible relations that are neither reflexive nor irreflexive are:
- {(1, 1)}
- {(1, 1), (1, 2)}
- {(1, 1), (2, 1)}
- {(1, 1), (1, 2), (2, 1)}
- {(2, 2)}
- {(2, 2), (2, 1)}
- {(2, 2), (1, 2)}
- {(2, 2), (2, 1), (1, 2)}
Therefore, the total count is 8.
Input: N = 3
Output: 384
Approach: The given problem can be solved based on the following observations:
- A relation R on a set A is a subset of the cartesian product of a set, i.e., A * A with N2 elements.
- A relation will be non-reflexive if it doesn’t contain at least one pair of (x, x) and relation will be non-irreflexive if it contains at least one pair of (x, x) where x € R.
- It can be concluded that the relation will be non-reflexive and non-irreflexive if it contains at least one pair of (x, x) and at most (N – 1) pairs of (x, x).
- Among N pairs of (x, x), the total number of possibilities of choosing any number of pairs except 0 and N – 1 is (2N – 2). For the remaining (N2 – N) elements, each element has two choices i.e., either to include or exclude it in the subset.
From the above observations, the total number of relations that are neither reflexive nor irreflexive on a set of first N natural numbers is given by 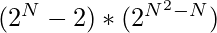 .
.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
const int mod = 1000000007;
int power(long long x, unsigned int y)
{
int res = 1;
x = x % mod;
if (x == 0)
return 0;
while (y > 0) {
if (y & 1)
res = (res * x) % mod;
y = y >> 1;
x = (x * x) % mod;
}
return res;
}
void countRelations(int N)
{
cout << (power(2, N) - 2)
* power(2, N * N - N);
}
int main()
{
int N = 2;
countRelations(N);
return 0;
}
|
Java
import java.io.*;
import java.lang.*;
import java.util.*;
class GFG{
static int mod = 1000000007;
static int power(int x, int y)
{
int res = 1;
x = x % mod;
if (x == 0)
return 0;
while (y > 0)
{
if ((y & 1) != 0)
res = (res * x) % mod;
y = y >> 1;
x = (x * x) % mod;
}
return res;
}
static void countRelations(int N)
{
System.out.print((power(2, N) - 2) *
power(2, N * N - N));
}
public static void main(String[] args)
{
int N = 2;
countRelations(N);
}
}
|
Python3
mod = 1000000007
def power(x, y):
res = 1
x = x % mod
if(x == 0):
return 0
while(y > 0):
if (y % 2 == 1):
res = (res * x) % mod
y = y >> 1
x = (x * x) % mod
return res
def countRelations(N):
print((power(2, N) - 2) * power(2, N * N - N))
N = 2
countRelations(N)
|
C#
using System;
class GFG{
static int mod = 1000000007;
static int power(int x, int y)
{
int res = 1;
x = x % mod;
if (x == 0)
return 0;
while (y > 0)
{
if ((y & 1) != 0)
res = (res * x) % mod;
y = y >> 1;
x = (x * x) % mod;
}
return res;
}
static void countRelations(int N)
{
Console.Write((power(2, N) - 2) *
power(2, N * N - N));
}
public static void Main(String[] args)
{
int N = 2;
countRelations(N);
}
}
|
Javascript
<script>
var mod = 1000000007;
function power(x, y)
{
var res = 1;
x = x % mod;
if (x == 0)
return 0;
while (y > 0) {
if (y %2 != 0)
res = (res * x) % mod;
y = y >> 1;
x = (x * x) % mod;
}
return res;
}
function countRelations(N)
{
document.write((power(2, N) - 2)
* power(2, (N * N) - N));
}
var N = 2;
countRelations(N);
</script>
|
Time Complexity: O(log N)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...