Number of possible pairs of Hypotenuse and Area to form right angled triangle
Last Updated :
31 May, 2022
Given two arrays H and S. The array H[] contains the length of the hypotenuse and the array S[] contains Area of a right-angled triangle. The task is to find all possible pairs of (H, S) such that we can construct a right-angled triangle with hypotenuse H and area S.
Examples:
Input : H[] = {1, 6, 4} ; S[] = {23, 3, 42, 14}
Output : 2
Possible pairs are {6, 3} {4, 3}
Input : H[] = {1, 6, 4, 3} ; S[] = {23, 3, 42, 5}
Output : 3
Possible pairs are {6, 3} {6, 5} {4, 3}
Say,
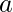 = Base of Right Angled Triangle
= Base of Right Angled Triangle
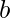 = Height of the Right Angled Triangle
= Height of the Right Angled Triangle
Therefore,
area S = (a*b)/2
or, 4*S*S=a*a*b*b
Also,
a2 + b2 = H2
Therefore,
4*S2 = a2(H2-a2)
Solving this quadratic equation in a2 and putting discriminant>=0 (condition for a to exist). We will get,
H2 >= 4*S
For a right-angled triangle to exist with
hypotenuse H and area S.
Naive Approach: The naive approach is to find all possible pairs of (H,S) and check if they satisfy the condition, H2 >= 4*S. Count the number of pairs that satisfies this condition and print the count.
Below is the implementation of the naive approach:
C++
#include <iostream>
using namespace std;
bool check(int H, int S)
{
return H * H >= 4 * S;
}
int findPairs(int H[], int n, int S[], int m)
{
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (check(H[i], S[j]))
count++;
}
}
return count;
}
int main()
{
int H[] = { 1, 6, 4 };
int n = sizeof(H)/sizeof(H[0]);
int S[] = { 23, 3, 42, 14 };
int m = sizeof(S)/sizeof(S[0]);
cout<<findPairs(H, n, S, m);
return 0;
}
|
Java
class GFG
{
static boolean check(int H, int S)
{
return H * H >= 4 * S;
}
static int findPairs(int H[], int n,
int S[], int m)
{
int count = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (check(H[i], S[j]))
count++;
}
}
return count;
}
public static void main(String args[])
{
int H[] = { 1, 6, 4 };
int n = H.length;
int S[] = { 23, 3, 42, 14 };
int m = S.length;
System.out.println(findPairs(H, n, S, m));
}
}
|
Python3
def check(H, S) :
return H * H >= 4 * S
def findPairs(H, n, S, m):
count = 0
for i in range(n) :
for j in range(m) :
if check(H[i], S[j]) :
count += 1
return count
if __name__ == "__main__" :
H = [ 1, 6, 4]
n = len(H)
S = [ 23, 3, 42, 14]
m = len(S)
print(findPairs(H, n, S,m))
|
C#
using System;
class GFG
{
static bool check(int H, int S)
{
return H * H >= 4 * S;
}
static int findPairs(int[] H, int n,
int[] S, int m)
{
int count = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (check(H[i], S[j]))
count++;
}
}
return count;
}
public static void Main()
{
int[] H = { 1, 6, 4 };
int n = H.Length;
int[] S = { 23, 3, 42, 14 };
int m = S.Length;
Console.Write(findPairs(H, n, S, m));
}
}
|
PHP
<?php
function check($H, $S)
{
return $H * $H >= 4 * $S;
}
function findPairs($H, $n, $S, $m)
{
$count = 0;
for ($i = 0; $i < $n; $i++)
{
for ($j = 0; $j < $m; $j++)
{
if (check($H[$i], $S[$j]))
$count++;
}
}
return $count;
}
$H = array( 1, 6, 4 );
$n = count($H);
$S = array( 23, 3, 42, 14 );
$m = count($S);
echo findPairs($H, $n, $S, $m);
?>
|
Javascript
<script>
function check(H , S)
{
return H * H >= 4 * S;
}
function findPairs(H , n , S , m)
{
var count = 0;
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
if (check(H[i], S[j]))
count++;
}
}
return count;
}
var H = [ 1, 6, 4 ];
var n = H.length;
var S = [ 23, 3, 42, 14 ];
var m = S.length;
document.write(findPairs(H, n, S, m));
</script>
|
Time Complexity: O(n*m) where n and m are the sizes of the array H and S respectively.
Auxiliary Space: O(1)
Efficient Approach: An efficient approach is to sort both the arrays available in increasing order. Then, for every possible length of the hypotenuse, apply Binary search to find the maximum area which satisfies the necessary condition.
Say, after the Binary search maximum possible area is available at index 4 in the array S[]. Then we can form 4 such possible pairs since all area less than that at index 4 will also be satisfying the condition.
Below is the implementation of the efficient approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool check(int H, int S)
{
return H * H >= 4 * S;
}
int findPairs(int H[], int n, int S[], int m)
{
int count = 0;
sort(H, H + n);
sort(S, S + m);
int index = -1;
for (int i = 0; i < n; i++) {
int start = 0;
int end = m - 1;
while (start <= end) {
int mid = start + (end - start) / 2;
if (check(H[i], S[mid])) {
index = mid;
start = mid + 1;
}
else {
end = mid - 1;
}
}
if (index != -1) {
count += index + 1;
}
}
return count;
}
int main()
{
int H[] = { 1, 6, 4 };
int n = sizeof(H)/sizeof(H[0]);
int S[] = { 23, 3, 42, 14 };
int m = sizeof(S)/sizeof(S[0]);
cout<<findPairs(H, n, S, m);
return 0;
}
|
Java
import java.util.Arrays;
import java.io.*;
class GFG {
static boolean check(int H, int S)
{
return H * H >= 4 * S;
}
static int findPairs(int H[], int n, int S[], int m)
{
int count = 0;
Arrays.sort(H);
Arrays.sort(S);
int index = -1;
for (int i = 0; i < n; i++) {
int start = 0;
int end = m - 1;
while (start <= end) {
int mid = start + (end - start) / 2;
if (check(H[i], S[mid])) {
index = mid;
start = mid + 1;
}
else {
end = mid - 1;
}
}
if (index != -1) {
count += index + 1;
}
}
return count;
}
public static void main (String[] args) {
int H[] = { 1, 6, 4 };
int n = H.length;
int S[] = { 23, 3, 42, 14 };
int m = S.length;
System.out.println(findPairs(H, n, S, m));
}
}
|
Python3
def check(H, S):
return H * H >= 4 * S;
def findPairs(H, n, S, m):
count = 0;
H.sort();
S.sort();
index = -1;
for i in range(n):
start = 0;
end = m - 1;
while (start <= end):
mid = int(start + (end - start) / 2);
if (check(H[i], S[mid])):
index = mid;
start = mid + 1;
else:
end = mid - 1;
if (index != -1):
count += index + 1;
return count;
H = [ 1, 6, 4 ];
n = len(H);
S= [ 23, 3, 42, 14 ];
m = len(S);
print(findPairs(H, n, S, m));
|
C#
using System;
public class GFG{
static bool check(int H, int S)
{
return H * H >= 4 * S;
}
static int findPairs(int []H, int n, int []S, int m)
{
int count = 0;
Array.Sort(H);
Array.Sort(S);
int index = -1;
for (int i = 0; i < n; i++) {
int start = 0;
int end = m - 1;
while (start <= end) {
int mid = start + (end - start) / 2;
if (check(H[i], S[mid])) {
index = mid;
start = mid + 1;
}
else {
end = mid - 1;
}
}
if (index != -1) {
count += index + 1;
}
}
return count;
}
static public void Main (){
int []H = { 1, 6, 4 };
int n = H.Length;
int []S = { 23, 3, 42, 14 };
int m = S.Length;
Console.WriteLine(findPairs(H, n, S, m));
}
}
|
PHP
<?php
function check($H, $S)
{
return $H * $H >= 4 * $S;
}
function findPairs($H, $n, $S, $m)
{
$count = 0;
sort($H);
sort($S);
$index = -1;
for ($i = 0; $i < $n; $i++)
{
$start = 0;
$end = $m - 1;
while ($start <= $end)
{
$mid = $start + (int)($end - $start) / 2;
if (check($H[$i], $S[$mid]))
{
$index = $mid;
$start = $mid + 1;
}
else
{
$end = $mid - 1;
}
}
if ($index != -1)
{
$count += $index + 1;
}
}
return $count;
}
$H = array( 1, 6, 4 );
$n = sizeof($H);
$S = array(23, 3, 42, 14 );
$m = sizeof($S);
echo findPairs($H, $n, $S, $m);
?>
|
Javascript
<script>
function check(H, S)
{
return H * H >= 4 * S;
}
function findPairs(H, n, S, m)
{
let count = 0;
H.sort(function(a, b){return a - b});
S.sort(function(a, b){return a - b});
let index = -1;
for (let i = 0; i < n; i++) {
let start = 0;
let end = m - 1;
while (start <= end) {
let mid = start +
parseInt((end - start) / 2, 10);
if (check(H[i], S[mid])) {
index = mid;
start = mid + 1;
}
else {
end = mid - 1;
}
}
if (index != -1) {
count += index + 1;
}
}
return count;
}
let H = [ 1, 6, 4 ];
let n = H.length;
let S = [ 23, 3, 42, 14 ];
let m = S.length;
document.write(findPairs(H, n, S, m));
</script>
|
Time Complexity: O(n*log(n)+m*log(m)+n*log(m)) where n and m are the sizes of the array H and S respectively. Here n*log(n) and m*log(m) are for sorting the array and n*log(m) is for traversing and applying binary search each time.
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...